
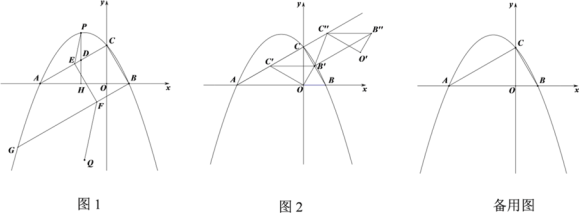
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
(1)如图1,求直线BC的解析式;
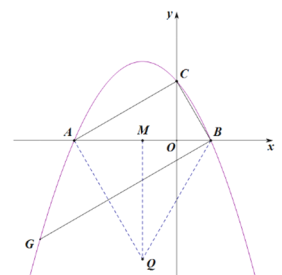
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)PE+EF+QF最小值为
;(2)PE+EF+QF最小值为 ![]() +2, E点坐标
+2, E点坐标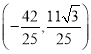 ;(3)能,
;(3)能,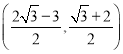 ,
,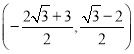 ,
,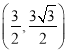 ,
,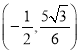
【解析】
(1)利用三角函数求出OC的长得到抛物线的解析式,求出图象与x轴的交点,设直线BC解析式为:![]() ,即可将点B、C的坐标代入求出答案;
,即可将点B、C的坐标代入求出答案;
(2)先求出直线AC的解析式,设点P、D的坐标,根据PD最大求得点P的坐标,利用勾股定理的逆定理及对称性得到△ABQ是等边三角形,过点Q作QM⊥x轴于点M,求出点Q的坐标,根据平移规律得到Q ′的坐标,连接P Q ′交AC于点E,再利用勾股定理求出![]() , 得到PE+EF+QF最小值= P Q ′+EF,由此求出答案;
, 得到PE+EF+QF最小值= P Q ′+EF,由此求出答案;
(3)根据点的位置分四种情况进行求解:①当![]() =
=![]() 时,②当
时,②当![]() =
=![]() 时,③当
时,③当![]() 时,④当
时,④当![]() 时,分别求出点C′′的坐标.
时,分别求出点C′′的坐标.
(1)在△BOC 中,OB=1,∠OBC=60°
∴BC=2,OC=![]() ,
,
∴抛物线解析式为:![]()
令y=0,得![]() ,
,
解之得![]() ,
,![]() ,
,
∴A(-3,0),B(1,0),C(0,![]() ),
),
设直线BC解析式为:![]() ,经过B(1,0),C(0,
,经过B(1,0),C(0,![]() ),
),
∴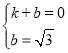 ,
,
得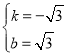 ,
,
∴![]() ;
;
(2)设直线AC解析式为:![]() ,经过A(-3,0),B(1,0),得
,经过A(-3,0),B(1,0),得![]() ,
,
设P点坐标为![]() ,则D点坐标为
,则D点坐标为![]() ,
,
∴PD=![]()
![]()
当![]() 时,PD有最大值,
时,PD有最大值,
∴P点坐标为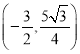 ,
,
在R△AOC中,可以求出AC=2![]() ,AB=4 ,
,AB=4 ,
∴AC2+BC2=12+4=16=AB2
由勾股定理逆定理得,可得∠ACB=90°,
可得∠CAB=30°=∠ABG,
由对称可得,AB=BQ=4, ∠ABQ=30°+30°=60°,
∴△ABQ是等边三角形,
过点Q作QM⊥x轴于点M,
∴MB=4,且OB=1
∴OM=1,QM=2![]()
∴Q点坐标为(-1,-2![]() )
)
由题意得,四边形BCEF是矩形,可得EF=BC=2,
将Q点沿射线EF方向平移2个单位(向左平移1个单位,向上平移![]() 个单位),可得Q ′的坐标为(-2,-
个单位),可得Q ′的坐标为(-2,-![]() )
)
连接P Q ′交AC于点E,点E即为所求,
P Q ′=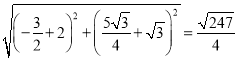
PE+EF+QF最小值= P Q ′+EF= ![]() +2,
+2,
直线P Q的解析式为:![]()
联立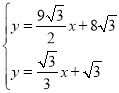 ,可得E点坐标
,可得E点坐标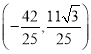
(3)存在,
∵A(-3,0),B(1,0),C(0,![]() ),
),
∴OA=3,OB=1,OC=![]() ,
,
∴![]() ,
,![]() ,
,
∴∠ACB=90°,
∴∠CAB=30°,AC=2![]() ,
,
∴,![]()
由旋转得到![]() ,
, ![]() ,
,
∵![]() ∥
∥![]() ,
,![]() =
=![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
①将三角形向上平移,当![]() =
=![]() 时,如图1,延长
时,如图1,延长![]() 交y轴于D,
交y轴于D,
∴四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴OD=OC+CD=![]() ,
,
∴![]()
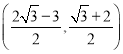 ;
;
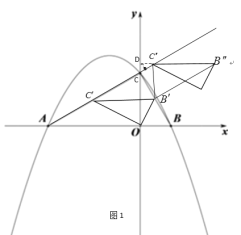
②将三角形向下平移,当![]() =
=![]() 时,如图2,则四边形
时,如图2,则四边形![]() 是菱形,
是菱形,
∴![]()
过点![]() 作
作![]() ⊥
⊥![]() ,
,
∵![]() ,
,
∴![]() =1,
=1,![]() ,
,
∴点![]() 的横坐标是
的横坐标是![]() ,纵坐标是
,纵坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是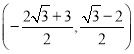 ;
;
③当![]() 时,如图3,
时,如图3,
则![]() ,
,
∵∠ACB=90°,
∴![]() ,
,
延长![]() 交y轴于D,
交y轴于D,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴OD=OC+CD=![]() ,
,
∴点![]() 的坐标是
的坐标是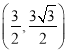 ;
;
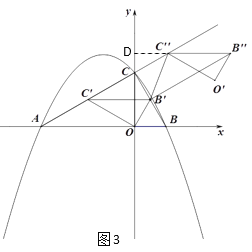
④当![]() 时,如图4,过点
时,如图4,过点![]() 作
作![]() ⊥
⊥![]() ,
,
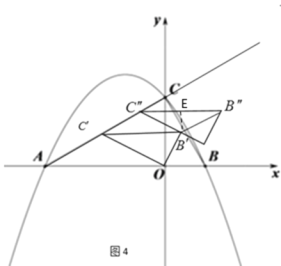
∴![]() ,
,
∴![]() ,
,
∴点![]() 的横坐标是
的横坐标是![]() ,纵坐标是
,纵坐标是![]() ,
,
∴点![]() 的坐标是
的坐标是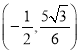 ,
,
综上,点![]() 的坐标是
的坐标是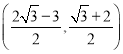 ,
,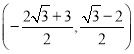 ,
,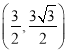 ,
, .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
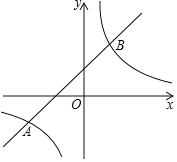
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2![]() 的图象相交于点A(﹣4,﹣2),B(m,4).
的图象相交于点A(﹣4,﹣2),B(m,4).
(1)求反比例函数和一次函数的表达式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车驾驶员坐在驾驶座位上,其视线观察不到的地方叫“汽车盲区”.如图是一辆汽车的“车头盲区”示意图,其中AC⊥BC,DE⊥BC,驾驶员所处位置的高度AC为1.4米,驾驶员座位AC与车头DE之间距离为2米,当驾驶员从A点观察车头D点时,其视线的俯角为12°,点A、D、B在同一直线上.
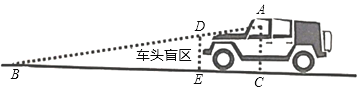
(1)请直接写出∠ABC的度数;
(2)求“车头盲区”点B、E之间的距离.(结果精确到0.1米)参考数据:sin12°=0.20,cas12°=0.99,tan12°=0.21
查看答案和解析>>
科目:初中数学 来源: 题型:
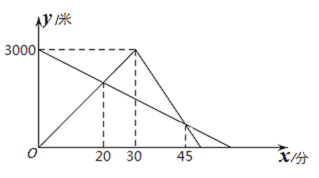
【题目】某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要____________分到达A地.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.
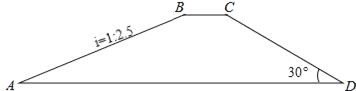
(1)求坝底AD的长度(结果精确到1米);
(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
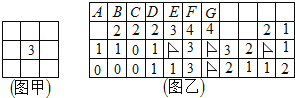
【题目】电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块己确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有
.(请填入方块上的字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
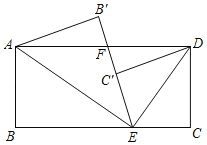
【题目】如图所示,在矩形ABCD中,AB=1,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,使点B落在B'处,线段EB'交AD于点F.将△ECD沿DE翻折,使点C的对应点C'落在线段EB'上,且点C'恰好为EB'的中点,则线段EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
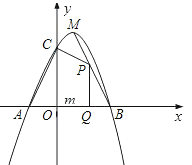
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,求出点
为等腰三角形?如果存在,求出点![]() 的坐标;如果不存在,请说呀理由.
的坐标;如果不存在,请说呀理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com