练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

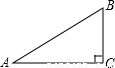
    某校要把一块形状是直角三角形的废地开发为生物园。如图所示，∠ACB=90°，AC=80m，BC=60m。若线段CD为一条水渠，且D在边AB上，已知水渠的造价是10元/米，则D点在距A点多远处时此水渠的造价最低？最低造价是多少？在图上标出D点。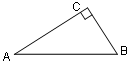
       

    480元，如下图

    解析试题分析：过C作CD⊥AB于D，先根据勾股定理求得AB的长，然后由直角三角形的面积公式根据等面积法即可求得CD的长，最后在Rt△ACD中根据勾股定理即可求得结果.
    解：过C作CD⊥AB于D

    ∵∠ACB=90°，AC=80m，BC=60m
    ∴AB==100m
    由面积相等得AB·CD=，解得CD=48
    在Rt△ACD中，AD==64
    距A点64m时造价最低，最低价是元.
    考点：垂线段最短的应用，勾股定理的应用
    点评：勾股定理的应用是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某校计划把一块近似于直角三角形的废地开发为生物园，如图所示，∠ACB=90°，BC=60米，∠A=36°，
    （1）若入口处E在AB边上，且与A、B等距离，求CE的长（精确到个位）；
    （2）若D点在AB边上，计划沿线段CD修一条水渠．已知水渠的造价为50元/米，水渠路线应如何设计才能使造价最低，求出最低造价．
    （其中sin36°=0.5878，cos36°=0.8090，tan36°=0.7265）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2014届云南红河弥勒西二中学八年级下学期期末测试数学试卷（解析版） 题型：解答题

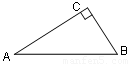
    某校要把一块形状是直角三角形的废地开发为生物园。如图所示，∠ACB=90°，AC=80m，BC=60m。若线段CD为一条水渠，且D在边AB上，已知水渠的造价是10元/米，则D点在距A点多远处时此水渠的造价最低？最低造价是多少？在图上标出D点。

       

     

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    某校要把一块形状是直角三角形的废地开发为生物园，如图所示，∠ACB=90°，AC=80m，BC=60m，若线段CD为一条水渠，且D在边AB上，已知水渠的造价是10元/米。
    则D点在距A点多远处时，此水渠的造价最低，最低造价是多少？

    查看答案和解析>>

    科目：初中数学 来源：2005年福建省厦门市五校联考数学试卷（解析版） 题型：解答题

    某校计划把一块近似于直角三角形的废地开发为生物园，如图所示，∠ACB=90°，BC=60米，∠A=36°，
    （1）若入口处E在AB边上，且与A、B等距离，求CE的长（精确到个位）；
    （2）若D点在AB边上，计划沿线段CD修一条水渠．已知水渠的造价为50元/米，水渠路线应如何设计才能使造价最低，求出最低造价．
    （其中sin36°=0.5878，cos36°=0.8090，tan36°=0.7265）

    查看答案和解析>>

    同步练习册答案