
【题目】已知抛物线y=x2+bx+c与x轴交于点A(﹣2,0)
(1)填空:c= ;(用含b的式子表示)
(2)b<4.
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),求b的取值范围;
(3)平移抛物线,使其顶点P落在直线y=3x﹣2上,设抛物线与直线的另一个交点为Q,C在该直线下方的抛物线上,求△CPQ面积的最大值.
【答案】(1)2b﹣4;(2)①详见解析;②﹣1<b≤0;(3)△CPQ面积的最大值为![]() .
.
【解析】
(1)将点A的坐标代入抛物线的解析式求解即可;
(2)①由(1)可知抛物线的解析式为y=x2+bx+2b4,然后证明△>0即可;
②当点B在点A的右侧时,0≤![]() <
<![]() ;当点B在点A的左侧时,4.5<
;当点B在点A的左侧时,4.5<![]() ≤4,从而可求得b的取值范围;
≤4,从而可求得b的取值范围;
(3)以平移后抛物线的顶点为坐标原点建立坐标系,则在新坐标系内抛物线的解析式为y=x2,直线的解析式为y=3x.过点C作CD∥y轴,交直线于点D.设点C的坐标为(x,x2),则点D的坐标为(x,3x),则DC=3xx2,然后建立三角形的面积与x的函数关系式求解即可.
解:(1)将点A的坐标代入y=x2+bx+c得:4﹣2b+c=0,
∴c=2b﹣4,
故答案为:2b﹣4;
(2)①由(1)可知抛物线的解析式为y=x2+bx+2b﹣4,
∴△=b2﹣4(2b﹣4)=b2﹣8b+16=(b﹣4)2,
又∵b<4,
∴△>0,
∴抛物线与x轴有两个交点;
②当点B在点A的右侧时.
∵线段AB上恰有5个整点,
∴0≤![]() <
<![]() ,即0≤﹣
,即0≤﹣![]() b<
b<![]() ,
,
∴﹣1<b≤0;
当点B在点A的左侧时,
∵线段AB上恰有5个整点,
∴﹣4.5<![]() ≤﹣4,即﹣4.5<﹣
≤﹣4,即﹣4.5<﹣![]() b≤﹣4.
b≤﹣4.
∴8≤b<9.
解得:﹣1<b≤0或8≤b<9,
又∵b<4,
∴b的取值范围是:﹣1<b≤0;
(3)如图所示:
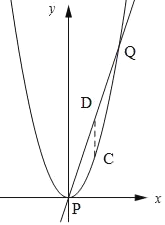
以平移后抛物线的顶点为坐标原点建立坐标系,则在新坐标系内抛物线的解析式为y=x2,直线的解析式为y=3x.
过点C作CD∥y轴,交直线于点D,
将y=3x代入y=x2得3x=x2,解得:x=0或x=3,
设点C的坐标为(x,x2),则点D的坐标为(x,3x),则DC=3x﹣x2,
∴△PQC的面积=![]() DC|xQ﹣xP|=
DC|xQ﹣xP|=![]() ×3×(3x﹣x2)=﹣
×3×(3x﹣x2)=﹣![]() x2+
x2+![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴△CPQ面积的最大值为![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
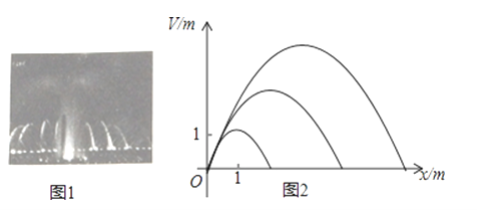
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
科目:初中数学 来源: 题型:
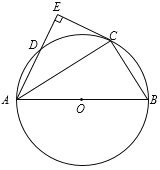
【题目】如图,AB是⊙O的直径,点C、D在圆上,![]() ,过点C作CE⊥AD交AD的延长线于点E.
,过点C作CE⊥AD交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)已知BC=3,AC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家限购以来,二手房和新楼盘的成交量迅速下降.据统计,某市限购前某季度二手房和新楼盘成交量为9500套;限购后,同一季度二手房和新楼盘的成交量共4425套.其中二手房成交量比限购前减少55%,新楼盘成交量比限购前减少52%.
(1)问限购后二手房和新楼盘各成交多少套?
(2)在成交量下跌的同时,房价也大幅跳水.某楼盘限购前均价为12000元/m2,限购后,房价经过二次下调后均价为9720元/m2![]() ,求平均每次下调的百分率.
,求平均每次下调的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,D是弧![]() 的中点,过点D作DE⊥AC交AC的延长线于点E.
的中点,过点D作DE⊥AC交AC的延长线于点E.
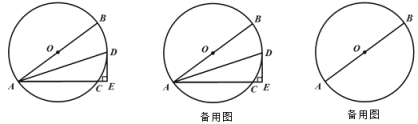
(1)求证:DE是⊙O的切线;
(2)当AB=10,AC=![]() 时,求弧
时,求弧![]() 的长;
的长;
(3)当AB=20时,直接写出△ABC面积最大时,点D到直径AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
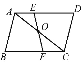
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
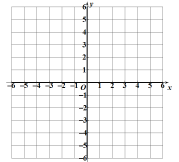
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
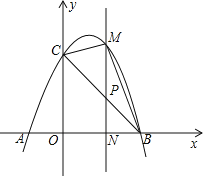
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)若点![]() 为线段
为线段![]() 上的一点(不与
上的一点(不与![]() 、
、![]() 重合),
重合),![]() 轴,且
轴,且![]() 交抛物线于点
交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 的面积最大时,求
的面积最大时,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com