
 如图,函数
如图,函数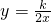 和
和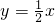 的图象相交于A、B两点,其中点A的横坐标为2.
的图象相交于A、B两点,其中点A的横坐标为2. 解:(1)∵A为两函数图象的交点,A点横坐标为2,把A点的横坐标代入y=
解:(1)∵A为两函数图象的交点,A点横坐标为2,把A点的横坐标代入y= x得,y=
x得,y= ×2=1,
×2=1, (k≠0),把A(2,1)代入得,
(k≠0),把A(2,1)代入得, ,k=2,
,k=2, ;
; ,
, ,
, ,
,
 =
= .
. ,0),P2(-
,0),P2(- ,0);
,0); ∴p4(-
∴p4(- ,0),
,0), ,0)、P2(-
,0)、P2(- ,0)、P3(-4,0)、p4(-
,0)、P3(-4,0)、p4(- ,0).
,0).

 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
 23、为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图象如图所示.
23、为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•相城区一模)如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点.
(2012•相城区一模)如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且P(-1,-2)为双曲线上的一点.查看答案和解析>>
科目:初中数学 来源:2009年江苏省苏州市相城区初三第一学期调研测试数学试卷(解析版) 题型:解答题
 的图象在第一象限内的交点,△AOB的面积为6,
的图象在第一象限内的交点,△AOB的面积为6,
查看答案和解析>>
科目:初中数学 来源:广东省中考真题 题型:解答题
| 如图,在Rt△ABC中,∠BAC=90°,∠C=60°,BC=24,点P是BC边上的动点(点P与点B、C不重合),过动点P作PD∥BA交AC于点D。 (1)若△ABC与△DPA相似,则∠APD是多少度? (2)试问:当PC等于多少时,△APD的面积最大?最大面积是多少? (3)若以线段AC为直径的圆和以线段BP为直径的圆相外切,求线段BP的长。 | |
 |
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《一次函数》(04)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com