
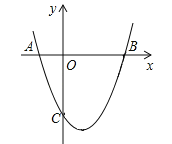
【题目】如图,抛物线与x轴的交点分别为A、B,与y轴的负半轴交于点C.已知抛物线的顶点坐标为(1,﹣4),点B的坐标(3,0).
(1)求该抛物线的解析式.
(2)在该函数图象上能否找到一点P,使PO=PC?若能,请求出点P的坐标;若不能,请说明理由.
【答案】(1) y=x2﹣2x﹣3;(2) 存在,P点坐标为(1+![]() ,﹣
,﹣![]() )或(1﹣
)或(1﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)可设出抛物线的顶点式,再利用B点坐标可求得抛物线解析式;
(2)由PO=PC可知点P在线段OC的垂直平分线上,则可知P点的纵坐标,代入抛物线解析式则可求得P点坐标.
(1)∵抛物线的顶点坐标为(1,﹣4),∴可设抛物线解析式为y=a(x﹣1)2﹣4.
∵抛物线过点B(3,0),∴0=a(3﹣1)2﹣4,解得:a=1,∴抛物线解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)存在.
∵PO=PC,∴点P在线段OC的垂直平分线上,在y=x2﹣2x﹣3中,令x=0可得:y=﹣3,∴C(0,﹣3),∴P点纵坐标为﹣![]() ,在y=x2﹣2x﹣3中,令y=﹣
,在y=x2﹣2x﹣3中,令y=﹣![]() 可得:x2﹣2x﹣3=﹣
可得:x2﹣2x﹣3=﹣![]() ,解得:x=1±
,解得:x=1±![]() ,∴P点坐标为(1+
,∴P点坐标为(1+![]() ,﹣
,﹣![]() )或(1﹣
)或(1﹣![]() ,﹣
,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
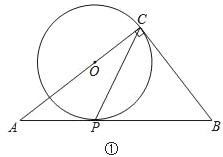
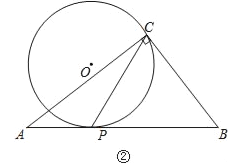
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市为创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶(如图所示),据调查该城市的A、B、C三个社区积极响应号并购买,具体购买的数和总价如表所示.
社区 | 甲型垃圾桶 | 乙型垃圾桶 | 总价 |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
(1)运用本学期所学知识,列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元?
(2)按要求各个社区两种类型的垃圾桶都要有,则a= .

查看答案和解析>>
科目:初中数学 来源: 题型:
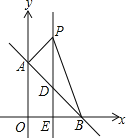
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
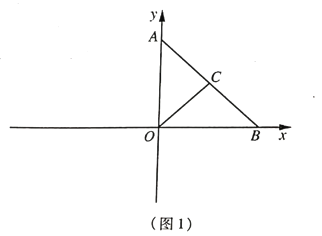
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() .
.
(1)如图1,求点![]() 的纵坐标;
的纵坐标;
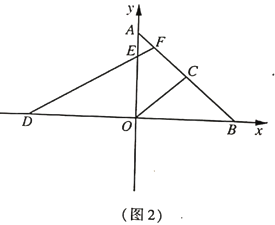
(2)如图2,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),点
的左侧),点![]() 在
在![]() 上,连接
上,连接![]() 交
交![]() 于点
于点![]() ;若
;若![]() ,求证:
,求证:![]()
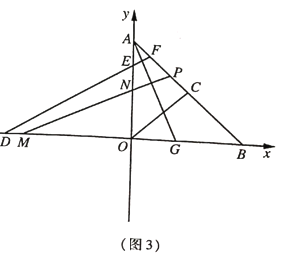
(3)如图3,在(2)的条件下,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
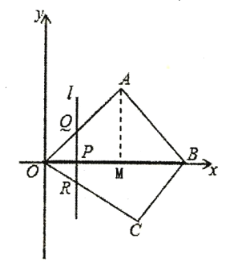
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 在第一象限,点
在第一象限,点![]() 在第四象限,点
在第四象限,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.![]() 且
且![]() ,
,![]() ,
,![]() 的长分别是二元一次方程组
的长分别是二元一次方程组![]() 的解(
的解(![]() ).
).
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,交边
,交边![]() 或边
或边![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() .已知
.已知![]() 时,直线
时,直线![]() 恰好过点
恰好过点![]() .
.
①当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②当![]() 时,求点
时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
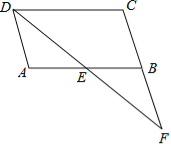
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com