
已知:二次函数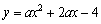
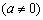 的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)①填空:二次函数图象的对称轴为 ;
②求二次函数的解析式;
(2) 点D的坐标为(-2,1),点P在二次函数图象上,∠ADP为锐角,且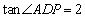 ,求点P的横坐标;
,求点P的横坐标;
(3)点E在x轴的正半轴上,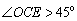 ,点O与点
,点O与点 关于EC所在直线对称.作
关于EC所在直线对称.作 ⊥
⊥ 于点N,交EC于点M.若EM·EC=32,求点E的坐标.
于点N,交EC于点M.若EM·EC=32,求点E的坐标.
 |
解:(1)①该二次函数图象的对称轴为直线 ;
;
②∵ 当x=0时,y=-4,
∴ 点C的坐标为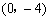 .
.
∵ 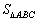

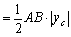 =12,
=12,
∴ AB=6.
又∵点A,B关于直线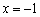 对称,
对称,
∴ A点和B点的坐标分别为 ,
,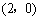 .
.
∴ 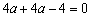 .解得
.解得 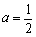 .
.
∴ 所求二次函数的解析式为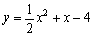 .
.
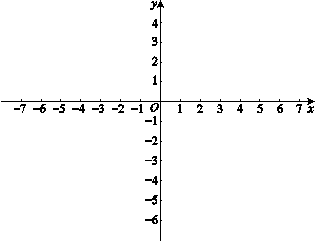
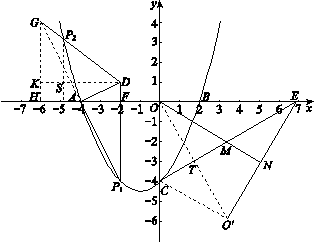
(2)如图,作DF⊥x轴于点F.分两种情况:
(ⅰ)当点P在直线AD的下方时,如图所示.
由(1)得点A ,点D
,点D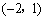 ,
,
∴ DF=1,AF=2.
在Rt△ADF中,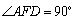 ,得
,得 .
.
延长DF与抛物线交于点P1,则P1点为所求.
∴ 点P1的坐标为 .
.
(ⅱ)当点P在直线AD的上方时,延长P1A至点G使得AG=AP1,连接DG,作GH⊥x轴于点H,如图所示.
可证 △GHA≌△ .
.
∴ HA =AF,GH = P1 F,GA =P1A.
 又∵
又∵  ,
,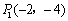 ,
,
∴ 点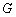 的坐标是
的坐标是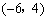 .
.
在△ADP1中,
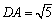 ,DP1=5,
,DP1=5,
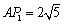 ,
,
∴  .
.
∴  .
.
∴ DA⊥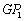 .
.
∴  .
.
∴ 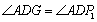 .
.
∴ 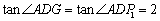 .
.
设DG与抛物线的交点为P2,则P2点为所求 .
.
作DK⊥GH于点K,作P2S∥GK交DK于点S.
设P2点的坐标为 ,
,
则 ,
,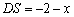 .
.
由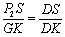 ,
, ,
,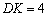 ,得
,得 .
.
整理,得 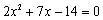 .
.
解得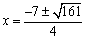 .
.
∵ P2点在第二象限,
∴ P2点的横坐标为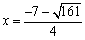 (舍正).
(舍正).
 综上,P点的横坐标为-2或
综上,P点的横坐标为-2或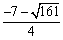 .
.
(3)如图,连接O ,交CE于T.连接
,交CE于T.连接 C.
C.
∵ 点O与点 关于EC所在直线对称,
关于EC所在直线对称,
∴ O ⊥CE,
⊥CE,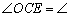
 CE,∠C
CE,∠C E
E 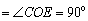 .
.
∴  C⊥
C⊥ E.
E.
∵ ON⊥ E,
E,
∴  C∥
C∥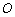 N.
N.
∴ 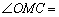
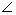
 C E
C E 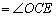 .
.
∴ 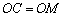 .
.
∴ 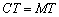 .
.
∵ 在Rt△ETO中, ,
,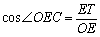 ,
,
在Rt△ 中,
中,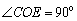 ,
, ,
,
∴ 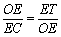 .
.
∴ 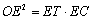

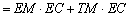
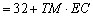 .
.
同理 
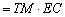
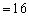 .
.
∴  .
.
∵  ,
,
∴ 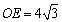 .
.
∵ 点E在x轴的正半轴上,
∴ E点的坐标为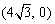 ).
).


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
小亮暑假期间去上海参观世博会,决定上午从中国馆(用A表示,下同)和韩国馆(B)中随机选一个馆参观,下午再从日本馆(C)、非洲馆(D)、法国馆(E)中随机选一个参观,求小亮全天参观的都是亚洲国家展馆的概率是多少?(要求写出用列表法或画树状图法求解的过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
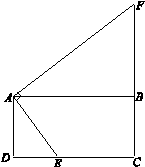
如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE交CB的延长线于点F.
(1)求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,
①求点M到FC的距离(用含x的代数式表示);
②连接BM,设 ,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
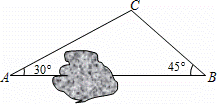
.如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com