Question

两条船分别从河的两岸同时相对开出，它们的速度各自一定，第一次相遇在距河的一岸800米（m）处，然后继续前进，各自到达对岸后立即折回，第二次相遇在距河的另一岸600米处，如果认定船到对岸反向航行时不耽误时间，并且不考虑水流速度，问河宽有多少米？

Answer 1

解：设河面宽度为xm，设一船速度为a，另一船速度为b，
则由题目中第一次相遇在距河的一岸800米（m）处时两船行驶时间相同，
则有：，
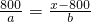
即：，
又有第二次相遇在距河的另一岸600米处同理可知：=，
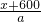
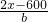
即：=，
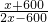
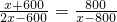
所以有：，化简得x（x-1800）=0，
解得：x=1800m或x=0（舍去），
答：河面宽为1800米．
故答案为：1800米．
分析：要求出河面宽度为多少，可以先假设出未知数，再找出题目中所给的等量关系，即：两船的速度分别各自一定，再根据等量关系列出方程求解作答．
点评：此类问题解题关键在于读懂题目的意思，根据题目给出的条件，找出合适的等量关系，再根据这一等量关系列出方程，再求解．