
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖЅЕузјБъЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЎ
жсЩЯЃЎ![]() ЪЧ
ЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЗжБ№гыжБЯп
жсЕФДЙЯпЗжБ№гыжБЯп![]() КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓЯпЖЮ
ЪБЃЌЧѓЯпЖЮ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ4ЃЉШєжБЯп![]() гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ
гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ![]() ЃЌЮЪЪЧЗёДцдкЕу
ЃЌЮЪЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)![]() ЃЌ
ЃЌ![]() ЃЛ(2)
ЃЛ(2)![]() ЃЛ(3) DEЕФзюДѓжЕЮЊ
ЃЛ(3) DEЕФзюДѓжЕЮЊ![]() ЃЛ(4)ДцдкЃЌЕу
ЃЛ(4)ДцдкЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ(
Лђ(![]() )Лђ(
)Лђ(![]() ЃЌ0)
ЃЌ0)
ЁОНтЮіЁП
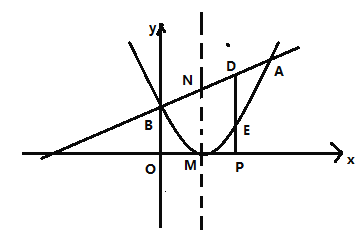
(1)ИљОнжБЯп![]() ОЙ§ЕуA(3ЃЌ4)ЧѓЕУm=1ЃЌИљОнЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊM(1ЃЌ0)ЃЌЧвОЙ§ЕуA(3ЃЌ4)МДПЩЧѓНтЃЛ
ОЙ§ЕуA(3ЃЌ4)ЧѓЕУm=1ЃЌИљОнЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊM(1ЃЌ0)ЃЌЧвОЙ§ЕуA(3ЃЌ4)МДПЩЧѓНтЃЛ
(2)ЯШЧѓЕУЕу![]() ЕФзјБъЃЌЕуDЕФзјБъЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМДПЩЧѓНтЃЛ
ЕФзјБъЃЌЕуDЕФзјБъЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМДПЩЧѓНтЃЛ
(3)гЩЬтвтЕУ![]() ЃЌдђ
ЃЌдђ![]() ИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЛ
ИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЛ
(4)ЗжСНжжЧщПіЃКDЕудкEЕуЕФЩЯЗНЁЂDЕудкEЕуЕФЯТЗНЃЌЗжБ№ЧѓНтМДПЩЃЎ
(1)ЁпжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЮЊ![]() ЃЌ
ЃЌ
ЁрЩшЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃК![]()
ЁпХзЮяЯпОЙ§![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃК![]() ЃЛ
ЃЛ
(2)Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЁрЕуDЕФзјБъЮЊ(2ЃЌ3)ЃЌ
Ёр![]() ЃЌ
ЃЌ

Ёр![]() ЃЛ
ЃЛ
(3)гЩЬтвтЕУ![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЁрЕБ
ЁрЕБ![]() (Ъєгк
(Ъєгк![]() ЗЖЮЇ)ЪБЃЌDEЕФзюДѓжЕЮЊ
ЗЖЮЇ)ЪБЃЌDEЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
(4) ТњзуЬтвтЕФЕуPЪЧДцдкЕФЃЌРэгЩШчЯТЃК
ЁпжБЯпABЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЮЊ(1ЃЌ2)ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпвЊЪЙЫФБпаЮЮЊЦНааЫФБпаЮжЛвЊ![]() ЃЌ
ЃЌ
ЁрЗжСНжжЧщПіЃК
ЂйDЕудкEЕуЕФЩЯЗНЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() (ЩсШЅ)Лђ
(ЩсШЅ)Лђ![]() ЃЛ
ЃЛ
ЂкDЕудкEЕуЕФЯТЗНЃЌдђ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]()
злЩЯЫљЪіЃЌТњзуЬтвтЕФЕуPЪЧДцдкЕФЃЌЕуPЕФзјБъЮЊ![]() Лђ(
Лђ(![]() )Лђ(
)Лђ(![]() ЃЌ0) ЃЎ
ЃЌ0) ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЮгОЪЧвЛЯюЩюЪмЧрЩйФъЯВАЎЕФЬхг§дЫЖЏ,ФГжабЇЮЊСЫМгЧПбЇЩњЕФгЮгОАВШЋвтЪЖЃЌзщжЏбЇЩњЙлПДСЫМЭЪЕЦЌЁАКЂзгЃЌЧыВЛвЊЫНздЯТЫЎЁБЃЌВЂгкЙлПДКѓдкБОаЃЕФ![]() УћбЇЩњжазїСЫГщбљЕїВщЃЎжЦзїСЫЯТУцСНИіВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнетСНИіЭГМЦЭМЛиД№вдЯТЮЪЬт:
УћбЇЩњжазїСЫГщбљЕїВщЃЎжЦзїСЫЯТУцСНИіВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнетСНИіЭГМЦЭМЛиД№вдЯТЮЪЬт:

(I)етДЮГщбљЕїВщжа,ЙВЕїВщСЫ УћбЇЩњЃЛ
(2)ВЙШЋСНИіЭГМЦЭМЃЛ
(3)ИљОнГщбљЕїВщЕФНсЙћЃЌЙРЫуИУаЃ![]() УћбЇЩњжаДѓдМгаЖрЩйШЫЁАНсАщЪБЛсЯТКгбЇгЮгОЁБ?
УћбЇЩњжаДѓдМгаЖрЩйШЫЁАНсАщЪБЛсЯТКгбЇгЮгОЁБ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧЖўДЮКЏЪ§yЃНax2+bx+cЭМЯѓЕФвЛВПЗжЃЌЦфЖдГЦжсЪЧxЃНЉ1ЃЌЧвЙ§Еу(Љ3ЃЌ0)ЃЌЯТСаЫЕЗЈЃКЂйabcЃМ0ЃЛЂк2aЉbЃН0ЃЛЂлШє(Љ5ЃЌy1)ЃЌ(3ЃЌy2)ЪЧХзЮяЯпЩЯСНЕуЃЌдђy1ЃНy2ЃЛЂм4a+2b+cЃМ0ЃЌЦфжаЫЕЗЈе§ШЗЕФЃЈЁЁЁЁЃЉ
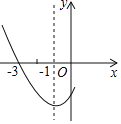
A.ЂйЂкB.ЂйЂкЂлC.ЂйЂкЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧ
ЪЧ![]() ЕФЗДБШР§КЏЪ§ЃЌЯТБэИјГіСЫ
ЕФЗДБШР§КЏЪ§ЃЌЯТБэИјГіСЫ![]() гы
гы![]() ЕФвЛаЉжЕЃЎ
ЕФвЛаЉжЕЃЎ
| Ё | -4 | -2 | -1 | 1 | 3 | 4 | Ё | ||
| Ё | -2 | 6 | 3 | Ё |
ЃЈ1ЃЉЧѓГіетИіЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉИљОнКЏЪ§БэДяЪНЭъГЩЩЯБэЃЛ
ЃЈ3ЃЉИљОнЩЯБэЃЌдкЯТЭМЕФЦНУцжБНЧзјБъЯЕжазїГіетИіЗДБШР§КЏЪ§ЕФЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХХЧђдЫЖЏдБеОдкЕуOДІСЗЯАЗЂЧђЃЌНЋЧђДгOЕуе§ЩЯЗН2mЕФAДІЗЂГіЃЌАбЧђПДГЩЕуЃЌЦфдЫааЕФИпЖШyЃЈmЃЉгыдЫааЕФЫЎЦНОрРыxЃЈmЃЉТњзуЙиЯЕЪНy=aЃЈx![]() kЃЉ2+hЃЎвбжЊЧђгыOЕуЕФЫЎЦНОрРыЮЊ6mЪБЃЌДяЕНзюИп2.6mЃЌЧђЭјгыOЕуЕФЫЎЦНОрРыЮЊ9mЃЎИпЖШЮЊ2.43mЃЌЧђГЁЕФБпНчОрOЕуЕФЫЎЦНОрРыЮЊ18mЃЌдђЯТСаХаЖЯе§ШЗЕФЪЧЃЈ ЃЉ
kЃЉ2+hЃЎвбжЊЧђгыOЕуЕФЫЎЦНОрРыЮЊ6mЪБЃЌДяЕНзюИп2.6mЃЌЧђЭјгыOЕуЕФЫЎЦНОрРыЮЊ9mЃЎИпЖШЮЊ2.43mЃЌЧђГЁЕФБпНчОрOЕуЕФЫЎЦНОрРыЮЊ18mЃЌдђЯТСаХаЖЯе§ШЗЕФЪЧЃЈ ЃЉ
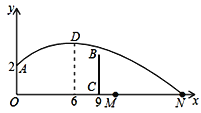
A. ЧђВЛЛсЙ§Эј B. ЧђЛсЙ§ЧђЭјЕЋВЛЛсГіНч
C. ЧђЛсЙ§ЧђЭјВЂЛсГіНч D. ЮоЗЈШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дк
дк![]() жсе§АыжсЩЯЃЉЃЌ
жсе§АыжсЩЯЃЉЃЌ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвУцЛ§ЮЊ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвУцЛ§ЮЊ![]() ЃЌЯжНЋХзЮяЯпби
ЃЌЯжНЋХзЮяЯпби![]() ЗНЯђЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЙ§Еу
ЗНЯђЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЙ§Еу![]() ЪБЃЌгы
ЪБЃЌгы![]() жсЕФСэвЛЕуЮЊ
жсЕФСэвЛЕуЮЊ![]() ЃЌЦфЖЅЕуЮЊ
ЃЌЦфЖЅЕуЮЊ![]() ЃЌЖдГЦжсгы
ЃЌЖдГЦжсгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
![]() СЌНг
СЌНг![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() ЪЧЗёЮЊЕШбќШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ЪЧЗёЮЊЕШбќШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
![]() ЯжНЋвЛзуЙЛДѓЕФШ§НЧАхЕФжБНЧЖЅЕу
ЯжНЋвЛзуЙЛДѓЕФШ§НЧАхЕФжБНЧЖЅЕу![]() ЗХдкЩфЯп
ЗХдкЩфЯп![]() ЛђЩфЯп
ЛђЩфЯп![]() ЩЯЃЌвЛжБНЧБпЪМжеЙ§Еу
ЩЯЃЌвЛжБНЧБпЪМжеЙ§Еу![]() ЃЌСэвЛжБНЧБпгы
ЃЌСэвЛжБНЧБпгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЪЧЗёДцдкетбљЕФЕу
ЃЌЪЧЗёДцдкетбљЕФЕу![]() ЃЌЪЙвдЕу
ЃЌЪЙвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮгы
ЮЊЖЅЕуЕФШ§НЧаЮгы![]() ШЋЕШЃПШєДцдкЃЌЧѓГіЕу
ШЋЕШЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЛ§МЋЯьгІЕГКЭЙњМвОЋзМЗіЦЖеНТдМЦЛЎЃЌФГЙЋЫОдкХЉДхзтгУСЫ 720ФЖЯажУЭСЕижжжВСЫЧЧ ФОаЭЁЂаЁЧЧФОаЭКЭЙрФОаЭШ§жжВшЪї. ЮЊДяЕНзюМбжжжВЪевцЃЌвЊЧѓжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧаЁЧЧФОаЭВшЪїУцЛ§ЕФ2БЖЃЌЙрФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§ЧЧФОаЭВшЪїУцЛ§ЕФ![]() БЖЃЌЕЋжжжВЧЧФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§270ФЖ. ЕНВшвЖВЩеЊМОНкЪБЃЌИУЙЋЫОЦИЧыЕБЕиХЉУёНјааВЩеЊЃЌУПШЫУПЬьПЩвдВЩеЊ0.4ФЖЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.5ФЖаЁЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.6ФЖЙрФОаЭВшвЖ. ШєИУЙЋЫОЦИЧывЛХњХЉУёЧЁКУ20ЬьФмВЩеЊЭъЫљгаВшвЖЃЌдђжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧ________ФЖ.
БЖЃЌЕЋжжжВЧЧФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§270ФЖ. ЕНВшвЖВЩеЊМОНкЪБЃЌИУЙЋЫОЦИЧыЕБЕиХЉУёНјааВЩеЊЃЌУПШЫУПЬьПЩвдВЩеЊ0.4ФЖЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.5ФЖаЁЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.6ФЖЙрФОаЭВшвЖ. ШєИУЙЋЫОЦИЧывЛХњХЉУёЧЁКУ20ЬьФмВЩеЊЭъЫљгаВшвЖЃЌдђжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧ________ФЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌEЪЧCDЕФжаЕуЃЌСЌНгOEЃЎЙ§ЕуCзїCFЁЮBDНЛЯпЖЮOEЕФбгГЄЯпгкЕуFЃЌСЌНгDFЃЎ
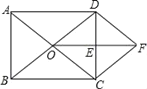
ЧѓжЄЃКЃЈ1ЃЉЁїODEЁеЁїFCEЃЛ
ЃЈ2ЃЉЫФБпаЮODFCЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
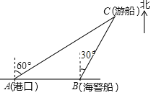
ЁОЬтФПЁПвЛЫвЙлЙтгЮДЌДгИлПк![]() вдББЦЋЖЋ
вдББЦЋЖЋ![]() ЕФЗНЯђГіИлЙлЙтЃЌКНаа
ЕФЗНЯђГіИлЙлЙтЃЌКНаа![]() КЃРяжС
КЃРяжС![]() ДІЪБЗЂЩњСЫВрЗГСДЌЪТЙЪЃЌСЂМДЗЂГіСЫЧѓОШаХКХЃЌвЛЫвдкИлПке§ЖЋЗНЯђЕФКЃОЏДЌНгЕНЧѓОШаХКХЃЌВтЕУЪТЙЪДЌдкЫќЕФББЦЋЖЋ
ДІЪБЗЂЩњСЫВрЗГСДЌЪТЙЪЃЌСЂМДЗЂГіСЫЧѓОШаХКХЃЌвЛЫвдкИлПке§ЖЋЗНЯђЕФКЃОЏДЌНгЕНЧѓОШаХКХЃЌВтЕУЪТЙЪДЌдкЫќЕФББЦЋЖЋ![]() ЗНЯђЃЌТэЩЯвд
ЗНЯђЃЌТэЩЯвд![]() КЃРяУПаЁЪБЕФЫйЖШЧАЭљОШдЎЃЌКЃОЏДЌЕНДяЪТЙЪДЌ
КЃРяУПаЁЪБЕФЫйЖШЧАЭљОШдЎЃЌКЃОЏДЌЕНДяЪТЙЪДЌ![]() ДІЫљашЕФЪБМфДѓдМЮЊ________аЁЪБЃЈгУИљКХБэЪОЃЉЃЎ
ДІЫљашЕФЪБМфДѓдМЮЊ________аЁЪБЃЈгУИљКХБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com