
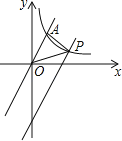
【题目】如图,在平面直角坐标系中,将直线![]() 向下平移后与反比例函数
向下平移后与反比例函数![]() 在第一象限内的图象交于点
在第一象限内的图象交于点![]() ,且
,且![]() 的面积为2,则平移后的直线的解析式是_____.
的面积为2,则平移后的直线的解析式是_____.
【答案】![]() .
.
【解析】
根据![]() 与
与![]() 相交于A点可先将A点坐标求出,设平移后的直线与y轴交于点B,作PM⊥OA,BN⊥OA,AC⊥y轴,进一步即可求出sin∠BON=
相交于A点可先将A点坐标求出,设平移后的直线与y轴交于点B,作PM⊥OA,BN⊥OA,AC⊥y轴,进一步即可求出sin∠BON=![]() ,然后根据
,然后根据![]() 的面积为2求出PM=
的面积为2求出PM=![]() ,最后利用三角函数求出OB的长进一步即可得出平移后的解析式.
,最后利用三角函数求出OB的长进一步即可得出平移后的解析式.
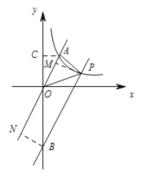
如图,设平移后的直线与y轴交于点B,作PM⊥OA,BN⊥OA,AC⊥y轴,
∵![]() 与
与![]() 相交于A点,∴A点坐标为(1,2),
相交于A点,∴A点坐标为(1,2),
∴OA=![]() ,sin∠BON=∠AOC=
,sin∠BON=∠AOC=![]() =
=![]() ,
,
∵△POA面积=![]() OAPM=
OAPM=![]()
![]() =2,
=2,
∴PM=![]() ,
,
∵PM⊥OA,BN⊥OA,
∴PM∥BN,
∵PB∥OA,
∴四边形BPMN为平行四边形,
∴BN=PM=![]() ,
,
∵sin∠BON=![]() =
=![]() =
=![]()
∴OB=4,
∴B点坐标为(0,![]() ),
),
∴平移后的直线解析式为:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
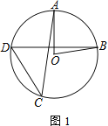
【题目】如图1,四边形ABCD内接于圆O,AC是圆O的直径,过点A的切线与CD的延长线相交于点P.且∠APC=∠BCP.
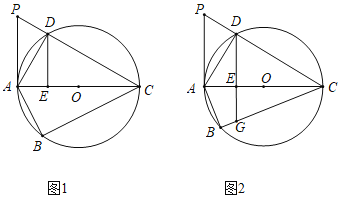
(1)求证:∠BAC=2∠ACD.
(2)过图1中的点D作DE⊥AC于E,交BC于G(如图2),BG:GE=3:5,OE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出
四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出![]() 厂家的合格率为
厂家的合格率为![]() ,并根据检测数据绘制了两幅不完整的统计图.
,并根据检测数据绘制了两幅不完整的统计图.

(1)抽查![]() 厂家的零件为______件,扇形统计图中
厂家的零件为______件,扇形统计图中![]() 厂家对应的圆心角为______.
厂家对应的圆心角为______.
(2)抽查![]() 厂家的合格零件为_______件.
厂家的合格零件为_______件.
(3)若要从![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出
四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出![]() ,
,![]() 两个厂家同时被选中的概率,并列出所有等可能的结果.
两个厂家同时被选中的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y1=x2﹣bx+c与直线y2=kx+m相交于A(﹣1,0),B(3,4)两点.
(1)请分别求出抛物线解析式和直线的解析式;
(2)直接写出y1﹣y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+x﹣
x2+x﹣![]() 与x轴相交于A,B两点,顶点为P.
与x轴相交于A,B两点,顶点为P.
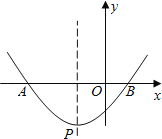
(1)求点A,点B的坐标;
(2)在抛物线上是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() (
(![]() ,1)为函数
,1)为函数![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() )与
)与![]() 的图象的交点.
的图象的交点.
(1)求![]() ;
;
(2)若函数![]() 的图象与
的图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() ,
,![]() ;
;
(3)若![]() ,设当
,设当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
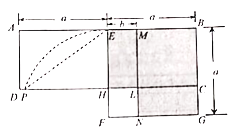
【题目】如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了![]() .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则
.现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个布袋中有红、黄、绿三种颜色的球各一个,从中先摸出一个球,记录下它的颜色,将它放回布袋,搅匀,再摸出一个球,记录下它的颜色.
(1)试用树形图或列表法中的一种列举出这两次摸出球的颜色所有可能的结果;
(2)求两次摸出球中至少有一个绿球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
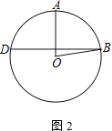
【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1) 若点C在优弧BD上,求∠ACD的大小
(2) 若点C在劣弧BD上,直接写出∠ACD的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com