
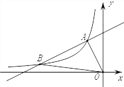
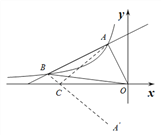
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)P点坐标为(
;(3)P点坐标为(![]() ,0)
,0)
【解析】分析:(1)由点A的坐标求反比例函数的解析式,得到点B的坐标,待定系数法求一次函数的解析式;(2)分别过点A,B用坐标轴的平行线构造矩形,用图形面积的和差关系求三角形AOB的面积;(3)作点A关于x轴的对称点A′,直线A′B与x轴的交点即是点P.
详解:(1)∵反比例![]() 的图象经过点A(—1,2),
的图象经过点A(—1,2),
∴![]() =—1×2=—2,
=—1×2=—2,
∴反比例函数表达式为:![]() ,
,
∵反比例![]() 的图象经过点B(—4,n),
的图象经过点B(—4,n),
∴—4n=—2,![]() ,∴B点坐标为(—4,
,∴B点坐标为(—4,![]() ),
),
∵直线![]() 经过点A(—1,2),点B(—4,
经过点A(—1,2),点B(—4,![]() ),
),
∴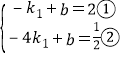 ,
,
①—②,得:3![]() ,∴
,∴![]() ,
,
把![]() 代入①,得:b=
代入①,得:b=![]() ,
,
∴一次函数表达式为:![]() .
.
(2)如图1所示,分别过点B作BD⊥x轴,垂足为D,过点A作AE⊥y轴,垂足为E,则四边形ODFE为矩形,
∵点A(—1,2),点B(—4,![]() ),
),
∴OD=EF=4,OE=DF=2,AE=1,BD=![]() ,
,
∴![]() ,
,![]() .
.
∵点A,点B在函数![]() 的图象上,∴
的图象上,∴![]()
∴![]() .
.
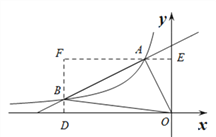
(3)如图2所示,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,
∵点A′和A(—1,2)关于x轴对称,∴点A′的坐标为(—1,—2),
设直线A′B的表达式为![]()
∵经过点A′(—1,—2),点B(—4,![]() ),∴
),∴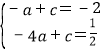
解得:![]() ,
,![]() .
.
∴直线A′B的表达式为:![]() .
.
当y=0时,则x=![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
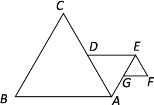
【题目】如图,作等边△ABC,取AC的中点D,以AD为边向△ABC形外作等边△ADE,取AE的中点G,再以EG为边作等边△EFG,如此反复,当作出第6个三角形时,若AB=4,整个图形的外围周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,∠A=∠B,E为AB的中点,连结CE,DE.
(1)求证:△ADE≌△BCE.
(2)若∠A=70°,∠BCE=60°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为边CD的中点,AE交BD于点O,若S△DOE=2,则平行四边形ABCD的面积为( )

A. 8B. 12C. 16D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
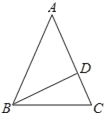
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com