
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
【答案】
(1)解:观察图象可知:(1)玲玲到达离家最远的地方是在12时,此时离家30千米
(2)解:10点半时开始第一次休息;休息了半小时
(3)解:玲玲郊游过程中,各时间段的速度分别为:
9~10时,速度为10÷(10﹣9)=10千米/时;
10~10.5时,速度约为(17.5﹣10)÷(10.5﹣10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30﹣17.5)÷(12﹣11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15﹣13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15﹣13)=15千米/小时
(4)解:玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时.
【解析】(1)离家最远可找最高点;(2)休息就是水平段,路程保持不变;(3)车速需要算每一倾斜段的路程及对应时间,夹角最大,速度最大.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,![]() ,
,![]() .若S=3,则
.若S=3,则![]() 的值为( )
的值为( )
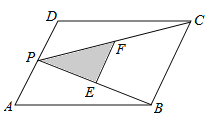
A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠3=∠4,∠E=90°,试问:AB∥CD吗?为什么?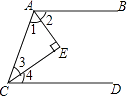
解:∵∠1+∠3+∠E=180°∠E=90°
∴∠1+∠3=
∵∠1=∠2,∠3=∠4
∴∠1+∠2+∠3+∠4=
∴AB∥CD .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ) 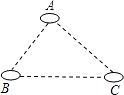
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( ) 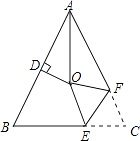
A.72°
B.100°
C.108°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com