
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ________.
________.

【答案】![]()
【解析】
判断出△ABE是等腰直角三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB=30°,再判断出△ABO是等边三角形,根据等边三角形的性质求出OB=AB,再求出OB=BE,然后根据等腰三角形两底角相等求出∠BOE=75°,再根据∠AOE=∠AOB+∠BOE计算即可得解.
解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB-∠CAE=45°-15°=30°,
∴∠BAO=90°-30°=60°,
∵矩形中OA=OB,
∴△ABO是等边三角形,
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∵∠OBE=∠ABC-∠ABO=90°-60°=30°,
∴∠BOE=![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠AOE=∠AOB+∠BOE,
=60°+75°,
=135°.
故答案为:135°.


科目:初中数学 来源: 题型:
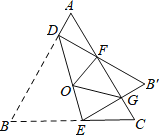
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 抛物线的对称轴是直线![]() B. 抛物线的顶点坐标是
B. 抛物线的顶点坐标是![]() C. 该二次函数有最小值
C. 该二次函数有最小值![]() D. 当
D. 当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com