
【题目】在平面直角坐标系xOy中,A(t,0),B![]() ,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
,对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
(1)若![]() ,在点C(0,
,在点C(0,![]() ),D
),D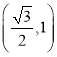 ,E
,E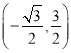 中,线段AB的“等角点”是 ;
中,线段AB的“等角点”是 ;
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(6,0),∠OMN=30°.
①线段AB的“等角点”P在直线MN上,且∠ABP=90°,求点P的坐标;
②在①的条件下,过点B作BQ⊥PA,交MN于点Q,求∠AQB的度数;
③若线段AB的所有“等角点”都在△MON内部,则t的取值范围是 .

【答案】(1)C、D;(2)①![]() ,②∠AQB=90°,③
,②∠AQB=90°,③![]()
【解析】
(1)根据给定的t值找出A、B点的坐标,再利用解三角形的方法讨论C、D、E点是否满足“等角点”的条件即可得出结论;
(2)①画出点N在y轴正半轴时图形,通过角的计算得出∠PAB=∠OMN,从而得出“PA=PM,AB=BM”,再通过解直角三角形即可得出P点的坐标,同理可得出点N在y轴负半轴时的P点的坐标;②通过角的计算找出∠BMQ=∠MQB=30°,再结合外角的性质得出BQ=BM=AB即得出△ABQ是等边三角形,从而得出结论,同理点N在y轴负半轴时,结论相同;
(3)通过构建与y轴以及与线段MN相切的圆,找出点A与点B的临界点,求出此时的t值,从而得出线段AB的所有“等角点”都在△MON内部,则t的取值范围.
(1)当t=﹣![]() 时,点A(﹣
时,点A(﹣![]() ,0),点B(
,0),点B(![]() ,0),
,0),
∵点C(0,![]() ),OC=
),OC=![]() =
=![]() AB,且点O为线段AB的中点,
AB,且点O为线段AB的中点,
∴△ABC为等边三角形,
∴∠ACB=60°,点C是线段AB的“等角点”;
∵点D(![]() ,1),B、D横坐标相等,
,1),B、D横坐标相等,
∴BD⊥x轴于点B.
∵AB=![]() ﹣(﹣
﹣(﹣![]() )=
)=![]() ,BD=1﹣0=1,tan∠ADB=
,BD=1﹣0=1,tan∠ADB=![]() =
=![]() ,
,
∴∠ADB=60°,点D是线段AB的“等角点”;
∵点E(﹣![]() ,
,![]() ),A、E横坐标相等,
),A、E横坐标相等,
∴AE⊥x轴于点A.
∵AB=![]() ﹣(﹣
﹣(﹣![]() )=
)=![]() ,AE=
,AE=![]() ﹣0=
﹣0=![]() ,tan∠AEB=
,tan∠AEB=![]() =
=![]() ,
,
∴∠AEB≠60°,点E不是线段AB的“等角点”.
综上可知:点C、D是线段AB的“等角点”.
故答案为:C、D.
(2)①当点N在y轴正半轴时,如图1,

∵∠APB=60°,∠ABP=90°,
∴∠PAB=30°,
又∵∠OMN=30°,
∴PA=PM,AB=BM.
∵AB=![]() ,
,
∴BM=![]() ,
,
∴PB=1.
∴P(6﹣![]() ,1).
,1).
当点N在y轴负半轴时,同理可得点![]() .
.
②当点N在y轴正半轴时,如图2,
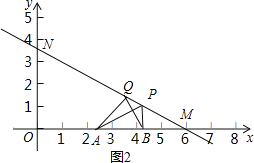
∵BQ⊥AP,且∠APB=60°,
∴∠PBQ=30°,
∴∠ABQ=60°,
∴∠BMQ=∠MQB=30°,
∴BQ=BM=AB,
∴△ABQ是等边三角形.
∴∠AQB=60°.
当点N在y轴负半轴时,同理可得∠AQB=90°.
③以AB=![]() 做底,AO′=BO′为腰,∠AO′B=120°作三角形,如图3所示.
做底,AO′=BO′为腰,∠AO′B=120°作三角形,如图3所示.
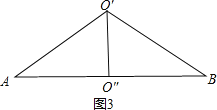
∵AO′=BO′,AB=![]() ,∠AO′B=120°,
,∠AO′B=120°,
∴AO′=1,O′O″=![]() .
.
(i)以直线y=![]() 上的点O′为圆心,1为半径作圆,当圆O′与y轴相切,且O′在y轴右侧时,如图4所示,
上的点O′为圆心,1为半径作圆,当圆O′与y轴相切,且O′在y轴右侧时,如图4所示,
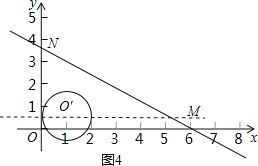
此时O′的坐标为(1,![]() ),此时A点的横坐标为1﹣
),此时A点的横坐标为1﹣![]() AB=1﹣
AB=1﹣![]() ,
,
即t=1﹣![]() ;
;
(ii)以直线y=![]() 上的点O′为圆心,1为半径作圆,当圆O′与线段MN相切,且O′在MN下方时,如图5所示.
上的点O′为圆心,1为半径作圆,当圆O′与线段MN相切,且O′在MN下方时,如图5所示.
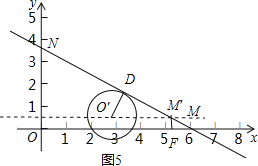
∵M′F=![]() ,∠OMN=30°,
,∠OMN=30°,
∴MF=![]() =
=![]() .
.
∵O′D=1,∠O′M′D=∠OMN=30°,
∴O′M′=![]() =2.
=2.
此时点B的横坐标为OM﹣MF﹣O′M′+![]() AB=4,
AB=4,
∴t+![]() =4,t=4﹣
=4,t=4﹣![]() .
.
综上可知:若线段AB的所有“等角点”都在△MON内部,则t的取值范围是1﹣![]() <t<4﹣
<t<4﹣![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】受非洲猪瘟的影响,2019年的猪肉价格创历史新高,同时其他肉类的价格也有一定程度的上涨,某超市11月份的猪肉销量是羊肉销量的![]() 倍,且猪肉价格为每千克
倍,且猪肉价格为每千克![]() 元羊肉价格为每千克
元羊肉价格为每千克![]() 元.
元.
(1)若该超市11月份猪肉、羊肉的总销售额不低于![]() 万元,则11月份的猪肉销量至少多少千克?
万元,则11月份的猪肉销量至少多少千克?
(2)12月份香肠腊肉等传统美食的制作,使得市场的猪肉需求加大,12月份猪肉的销量比11月份增长了![]() ,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了
,由于国家对猪肉价格的调控,12 月份的猪肉价格比11月份降低了![]() ,羊肉的销量是11月份猪肉销量的
,羊肉的销量是11月份猪肉销量的![]() ,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了
,且价格不变.最终,该超市12月份猪肉和.羊肉的销售额比11月份这两种肉的销售额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了如下框中的题目:

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=”).
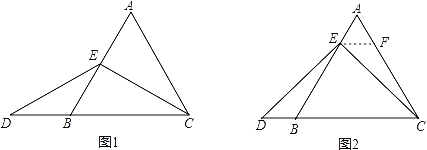
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个斜边长是8的Rt△AEC,一个斜边长是6的Rt△AFB,一个正方形AEDF,拼成一个如图所示的Rt△BCD,则Rt△AEC和Rt△AFB的面积之和是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
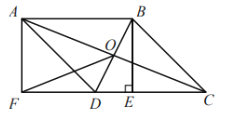
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
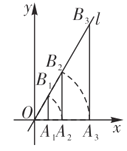
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交过原点与
轴的垂线交过原点与![]() 轴夹角为
轴夹角为![]() 的直线
的直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ……按此做法进行下去,则点
……按此做法进行下去,则点![]() 的坐标是_____.
的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①点D到∠BAC的两边距离相等;
②点D在AB的中垂线上;
③AD=2CD
④AB=2![]() CD
CD
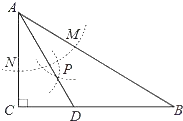
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
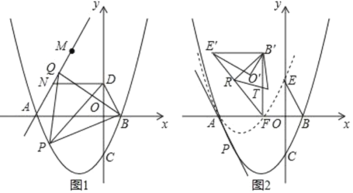
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com