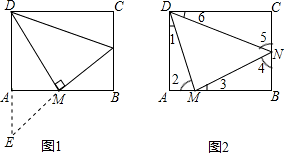
解:(1)有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似;
选△DAM∽△MBN,
证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠ADM=90°-∠AMD,
∵DM⊥MN,
∴∠BMN=180°-90°-∠AMD=90°-∠AMD,
∴∠ADM=∠BMD,
∴△DAM∽△MBN;
选△DAM∽△DMN,
证明:延长NM交DA的延长线于E点,如图1.
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,
∴∠EAM=∠B=90°,
又∵∠AME=∠BMN,AM=BM,
∴△AME≌△BMN,
∴EM=MN,
又∵DM⊥MN,
∴DE=DN,
∴∠ADM=∠NDM,
又∵∠DAM=∠DMN=90°,
∴△DAM∽△DMN;
选△DAM∽△MBN,
证明:延长MN交DA的延长线于E点,如图1.
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,
∴∠EAM=∠B=90°,
又∵∠AME=∠BMN,AM=BM,
∴△AME≌△BMN,
∴EM=MN,∠E=∠MNB,
又∵DM⊥MN,
∴DE=DN,
∴∠E=∠DNM,
∴∠DNM=∠MNB,
又∵∠DMN=∠B=90°,
∴△DMN∽△MBN;
(2)①如图2,AM=t,MB=5-t,BN=

t(0<t<5),
分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN,
∴
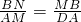
,
∴
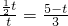
,
解得:t=

,
(Ⅱ)当∠2=∠3时,△DAM∽△NBM,
∴
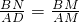
,
∴AM•BN=AD•BM,
∴t×

t=3(5-t),
解得:t
3=

-3,t
4=-

-3(不合题意舍去),
∴当t=

时,△DAM∽△MBN;当t=

-3时,△DAM∽△NBM.
②分四种情况:(Ⅰ)当∠1=∠3=∠6时,∠DMN=90°,△DAM∽△MBN∽△DCN,
由
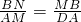
,
得:BN=
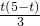
,
∴CN=
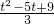
,
由
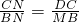
,得:CN•MB=DC•BN,
∴
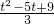
-(5-t)=5-
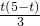
,
化简得:t
2-10t+9=0,解得:t
1=1,t
2=9(不合题意舍去),a=

,
(Ⅱ)当∠1=∠3=∠5时,
∵∠5+∠6=90°,
∴∠1+∠6=90°,(与已知条件矛盾)
所以此时不存在.
(Ⅲ)当∠2=∠3=∠6时,
方法一:∵∠1+∠2=90°,
∴∠1+∠6=90°,(与已知条件矛盾)所以此时不存在.
方法二:由
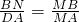
,
得:BN=
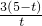
,
∴CN=
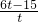
,
由
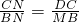
,得:CN•MB=DC•BN,
∴
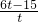
(5-t)=5-
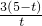
,
解得:t=5(不合题意舍去),所以此时不存在.
(Ⅳ)当∠2=∠3=∠5时,△DAM∽△NBM∽△DCN,
由(Ⅲ)得BN=
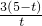
,
∴CN=
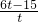
,
由
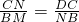
,得:CN•NB=DC•BM,
∴
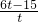
-
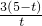
=5(5-t),
化简得:5t
2-18t+45=0方程没有实数根,所以此时不存在.
综上所述:当a=

时,△DAM∽△MBN∽△DCN.
分析:(1)首先可得有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似;然后选择其中的一对证明即可,注意应用矩形的性质,特别是同角或等角的余角相等的性质的应用;
(2)①如图2可得AM=t,MB=5-t,BN=

t(0<t<5),然后分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN与(Ⅱ)当∠2=∠3时,△DAM∽△NBM去分析根据相似三角形的对应边成比例,即可得方程,解方程即可求得答案;
②分四种情况去分析:(Ⅰ)当∠1=∠3=∠6时,∠DMN=90°,△DAM∽△MBN∽△DCN,(Ⅱ)当∠1=∠3=∠5时,(Ⅲ)当∠2=∠3=∠6时,(Ⅳ)当∠2=∠3=∠5时,△DAM∽△NBM∽△DCN,根据相似三角形的对应边成比例列方程求解即可求得答案.
点评:此题考查了相似三角形的判定与性质,矩形的性质,一元二次方程的解法,以及直角三角形的性质等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.

 个单位长度/秒,运动的时间为t秒.当t为何值时,△DAM与△MBN相似?请说明理由;
个单位长度/秒,运动的时间为t秒.当t为何值时,△DAM与△MBN相似?请说明理由;
 解:(1)有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似;
解:(1)有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似; t(0<t<5),
t(0<t<5),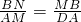 ,
,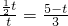 ,
, ,
,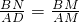 ,
, t=3(5-t),
t=3(5-t), -3,t4=-
-3,t4=- -3(不合题意舍去),
-3(不合题意舍去), 时,△DAM∽△MBN;当t=
时,△DAM∽△MBN;当t= -3时,△DAM∽△NBM.
-3时,△DAM∽△NBM.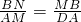 ,
,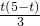 ,
,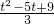 ,
,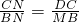 ,得:CN•MB=DC•BN,
,得:CN•MB=DC•BN,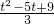 -(5-t)=5-
-(5-t)=5-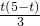 ,
, ,
,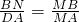 ,
,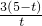 ,
,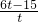 ,
,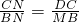 ,得:CN•MB=DC•BN,
,得:CN•MB=DC•BN,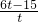 (5-t)=5-
(5-t)=5-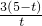 ,
,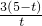 ,
,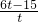 ,
,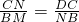 ,得:CN•NB=DC•BM,
,得:CN•NB=DC•BM,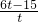 -
-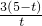 =5(5-t),
=5(5-t), 时,△DAM∽△MBN∽△DCN.
时,△DAM∽△MBN∽△DCN. t(0<t<5),然后分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN与(Ⅱ)当∠2=∠3时,△DAM∽△NBM去分析根据相似三角形的对应边成比例,即可得方程,解方程即可求得答案;
t(0<t<5),然后分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN与(Ⅱ)当∠2=∠3时,△DAM∽△NBM去分析根据相似三角形的对应边成比例,即可得方程,解方程即可求得答案;

 阅读快车系列答案
阅读快车系列答案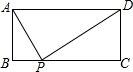 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( ) (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为