练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2006•济南）现有若干张边长不相等但都大于4cm的正方形纸片，从中任选一张，如图从距离正方形的四个顶点2cm处，沿45°角画线，将正方形纸片分成5部分，则中间阴影部分的面积是    cm2；若在上述正方形纸片中再任选一张重复上述过程，并计算阴影部分的面积，你能发现什么规律：    ．
    【答案】分析：根据已知求得阴影部分的边长，从而根据面积公式即可求得其面积．
    解答：解：辅助线如图所示，则中间的阴影正方形的边长为，其面积为（2）2=8，
    因为正方形纸片边长都大于4cm，因此猜想得到阴影部分的面积是8cm2，即阴影部分的面积不变．
    点评：本题考查正方形的性质与逻辑思维能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：044

    (2006，济南)元旦联欢会前某班布置教室，同学们利用彩纸条粘成一环套一环的彩纸链，小颖测量了部分彩纸链的长度，她得到的数据如下表：

    (1)把上表中x，y的各组对应值作为点的坐标，在如图所示的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式．

    (2)教室天花板对角线长10m，现需沿天花板对角线各拉一根彩纸链，则每根彩纸链至少要用多少个纸环?

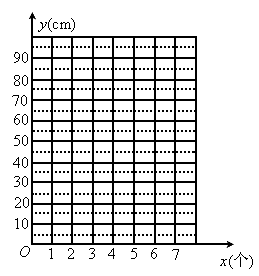
    查看答案和解析>>

    同步练习册答案