
如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作 APCD,AC与PD相交于点E,已知∠ABC=∠AEP=
APCD,AC与PD相交于点E,已知∠ABC=∠AEP=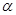 (0°<
(0°<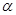 <90°).
<90°).
(1)求证: ∠EAP=∠EPA;
(2)  APCD是否为矩形?请说明理由;
APCD是否为矩形?请说明理由;
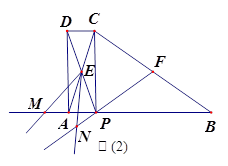
(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.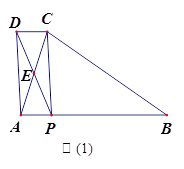
证明:(1)在△ABC和△AEP中, ∠ABC=∠AEP,∠BAC=∠EAP,
∠ABC=∠AEP,∠BAC=∠EAP,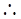 ∠ACB=∠APE,
∠ACB=∠APE,
在△ABC中,AB=BC.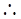 ∠ACB=∠BAC,
∠ACB=∠BAC, ∠EPA=∠EAP,
∠EPA=∠EAP,
(2)  APCD是矩形.
APCD是矩形. 四边形APCD是平行四边形,
四边形APCD是平行四边形, AC=2EA,PD=2EP.
AC=2EA,PD=2EP.
由(1)知, ∠EPA=∠EAP. EA=EP,进而AC=PD
EA=EP,进而AC=PD
 APCD是矩形.
APCD是矩形.
(3)EM=EN EA=EP,
EA=EP,  ∠EPA=90° -
∠EPA=90° - 
 ∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°-
∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°- )=90°+
)=90°+
由(2)知, ∠CPB=90°,F是BC的中点,  FP=FB,
FP=FB, ∠FPB=∠ABC=
∠FPB=∠ABC=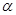 ,
, ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -
∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -  +
+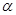 =90°+
=90°+
 ∠EAM=∠EPN
∠EAM=∠EPN ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,
∠AEP绕点E顺时针旋转适当的角度,得到∠MEN, ∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP.
∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP. △EAM≌△EPN,
△EAM≌△EPN, EM=EN.
EM=EN.
解析


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
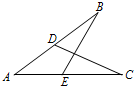 17、如图,D在AB上,E在AC上,且∠B=∠C,添加下列条件:①AD=AE;②∠AEB=∠ADC;③BE=CD之一,就能使△ABE≌△ACD,则符合这样要求的条件个数是( )
17、如图,D在AB上,E在AC上,且∠B=∠C,添加下列条件:①AD=AE;②∠AEB=∠ADC;③BE=CD之一,就能使△ABE≌△ACD,则符合这样要求的条件个数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com