
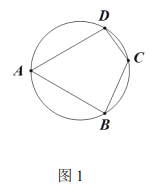
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
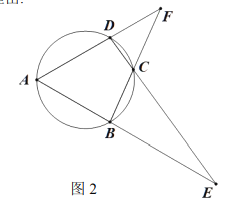
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
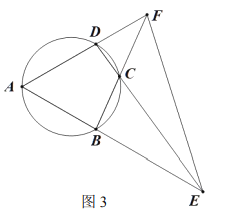
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)108;(3)存在,理由见解析
;(2)108;(3)存在,理由见解析
【解析】
(1)①连接BD,根据题意得出△ABD为等边三角形,再分别作△ABD三边的垂直平分线BE、DF、AM交于点O,则点O即为该圆的圆心,之后利用![]() 求出DM,由此进一步求解即可得出答案;②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,根据题意进一步证明△DCE为等边三角形,从而得出BC+CD=BC+CE=BE,然后进一步分析得出当
求出DM,由此进一步求解即可得出答案;②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,根据题意进一步证明△DCE为等边三角形,从而得出BC+CD=BC+CE=BE,然后进一步分析得出当![]() 时,BE最大,据此通过分析即可得出答案;
时,BE最大,据此通过分析即可得出答案;
(2)连接![]() ,根据题意首先证明∠1=∠F,∠2=∠E,从而得出
,根据题意首先证明∠1=∠F,∠2=∠E,从而得出![]() ,然后利用相似三角形性质得出
,然后利用相似三角形性质得出![]() ,据此即可求出
,据此即可求出![]() ;
;
(3)作点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,并连接
对称,并连接![]() ,
,![]() ,结合(2)中的证明得出
,结合(2)中的证明得出![]() ,由此可得
,由此可得![]() ,即
,即![]() ,据此,根据题意再接着证明
,据此,根据题意再接着证明![]() ,从而即可得出
,从而即可得出![]() 、
、![]() 、
、![]() 在同一直线上,即在线段
在同一直线上,即在线段![]() 上存在点
上存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
(1)
①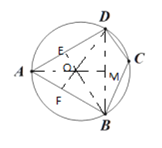
如图,连接BD,
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
再分别作△ABD三边的垂直平分线BE、DF、AM交于点O,则点O即为该圆的圆心,
∴AO=DO=BO=6,∠ODM=30°,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,
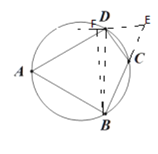
∵∠A=60°,
∴∠DCB=120°,
∴∠DCE=60°,
∵DC=CE,
∴△DCE为等边三角形,
∴∠E=60°,BC+CD=BC+CE=BE,
在Rt△BFE中,![]() ,
,
∵![]() ,
,
∴当![]() 时,BE最大,
时,BE最大,
∴此时![]() ,
,
∴四边形![]() 的周长最大值为:
的周长最大值为:![]() ,
,
故答案为:①![]() ;②
;②![]() ;
;
(2)如图,连接![]() ,
,
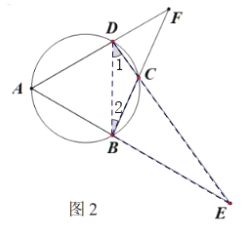
∵∠A=60°,AB=AD,四边形![]() 内接于圆,
内接于圆,
∴∠DCB=120°,∠ADB=∠ABD=60°,![]() ,
,
∴∠1+∠E=∠ABD=60°,![]() ,
,![]() ,
,
∴∠1=∠F,∠2=∠E,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)存在,理由如下:
如图,作点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,并连接
对称,并连接![]() ,
,![]() ,
,
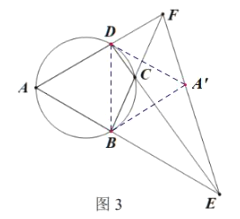
∵△ABD是等边三角形,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 60°,
60°,![]() 60°,
60°,![]() ,
,
∴![]() 60°,
60°,
由(2)可知:![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,
∴在线段![]() 上存在点
上存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,
轴上,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点,过点
边上一动点,过点![]() 的反比例函数
的反比例函数![]() 与边
与边![]() 交于点
交于点![]() .若将
.若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点
的对应点![]() 恰好落在对角线
恰好落在对角线![]() 上. 则反比例函数的解析式是( )
上. 则反比例函数的解析式是( )
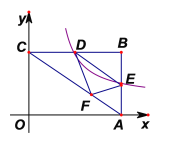
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在以BC为直径的⊙O上,连接AB、AC,点H为AB的中点.过点H的弦DE⊥BC于点F,连接CD、CH.
(1)求证:AB2=2BC·BF
(2)取AC的中点G,连接HG,过点D作线段DI与AC交于点J,与HJ的延长线交于点I.若AB=AG=4,求DJ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以![]() 为圆心,在第一象限内画圆弧,与双曲线交于两点,点
为圆心,在第一象限内画圆弧,与双曲线交于两点,点![]() 是圆弧上一个动点,连结
是圆弧上一个动点,连结![]() 并延长交第三象限的双曲线于点
并延长交第三象限的双曲线于点![]() ,作
,作![]() 轴,
轴,![]() 轴,只有当
轴,只有当![]() 时,
时,![]() ,则
,则![]() 的半径为_____________________.
的半径为_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
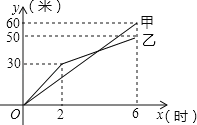
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
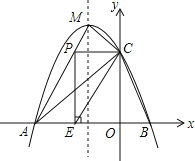
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点
与x轴交于A、B两点,与y轴交于点![]() ,且此抛物线的顶点坐标为
,且此抛物线的顶点坐标为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 设点D为已知抛物线对称轴上的任意一点,当
设点D为已知抛物线对称轴上的任意一点,当![]() 与
与![]() 面积相等时,求点D的坐标;
面积相等时,求点D的坐标;
![]() 点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将
点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将![]() 沿直线CE翻折,使点P的对应点
沿直线CE翻折,使点P的对应点![]() 与P、E、C处在同一平面内,请求出点
与P、E、C处在同一平面内,请求出点![]() 坐标,并判断点
坐标,并判断点![]() 是否在该抛物线上.
是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
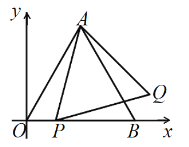
【题目】如图,平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,以
,以![]() 为边长,在
为边长,在![]() 的右侧作等边
的右侧作等边![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 与
与![]() 的函数关系式是________.
的函数关系式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
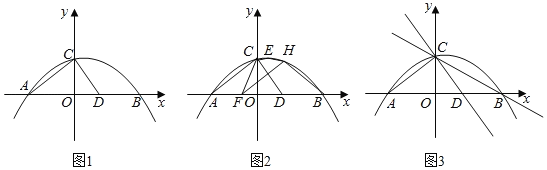
【题目】如图1,二次函数y![]() x2
x2![]() x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.
x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.
(1)求点D的坐标;
(2)如图2,已知点E是该二次函数图象的顶点,在线段AO上取一点F,过点F作FH⊥CD,交该二次函数的图象于点H(点H在点E的右侧),当五边形FCEHB的面积最大时,求点H的横坐标;
(3)如图3,在直线BC上取一点M(不与点B重合),在直线CD的右上方是否存在这样的点N,使得以C、M、N为顶点的三角形与△BCD全等?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com