
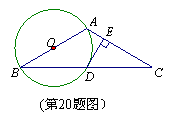
已知:如图,在⊿ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作![]() 于点E.
于点E.
(1)请说明DE是⊙O的切线;
(2)若![]() ,AB=8,求DE的长.
,AB=8,求DE的长.
解:(1)解法一:
连接OD,则OD=OB.
∴![]() ,
,
∵AB=AC,∴![]() .
.
∴![]() ,∴OD//AC
,∴OD//AC
∴![]() .
.
∴DE是⊙O的切线.
解法二:
连接OD,AD.
∵AB是⊙O的直径,∴![]() .
.
又∵AB=AC,∴BD=CD.
∵OA=OB,∴OD是△ABC的中位线.
∴OD//AC,∴![]() .
.
∴DE是⊙O的切线.
(2)连接AD(对应(1)的解法一)
∵AB是⊙O的直径,∴![]() .
.
∴![]() .
.
又∵AB=AC,∴CD=BD=![]() ,
,![]() .
.
∴![]()
解法二:
连接AD.
AB是⊙O的直径,∴![]() .
.
∴![]() . …
. …
又∵OA=OD,∴![]() .
.
∴![]() .
.
∴![]() .
.
…………………………11分
解法三:
连接AD.
AB是⊙O的直径,∴![]() . …
. …
又∵![]() .
.
![]() ∴⊿ADB∽⊿AED.
∴⊿ADB∽⊿AED.
∴![]() .
.
而![]() .
.
∴![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).
(1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.
已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com