已知直线y=-x+2与x轴和y轴交于点A和点B,另一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两个面积相等的三角形,求k和b的值.
分析:求得A(2,0),B(0,2),则△AOB是等腰直角三角形,而点C(1,0)是OA的中点.
一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两个面积相等的三角形,由此可知,该直线y=kx+b过点B.
然后把点B、C的坐标代入,利用方程组,即可求解.
解答:解:∵直线y=-x+2与x轴和y轴交于点A和点B,
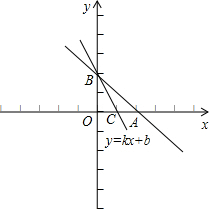
∴A(2,0),B(0,2),△AOB是等腰直角三角形
∵直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两个面积相等的三角形,而点C(1,0)是OA的中点
∴直线y=kx+b过点B(0,2),C(1,0),
∴
,
∴
.
点评:此类题目体现了数形结合的数学思想,主要利用待定系数法及方程组来解决问题.



 名校课堂系列答案
名校课堂系列答案