
【题目】综合与实践
旋转是图形变化的方法之一,借助旋转知识可以解决线段长、角的大小、取值范围、判断三角形形状等问题,在实际生活中也有着十分重要的地位和作用.
问题背景
一块等边三角形建筑材料内一点到三角形三个顶点的距离满足一定条件时,我们可以用所学的知识帮助工人师傅在没有刻度尺的情况下求出等边三角形的边长.
数学建模
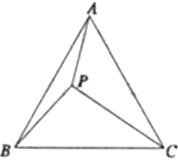
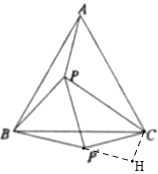
如图,等边三角形![]() 内有一点
内有一点![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
问题解决
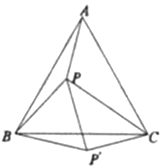
(1)如图,将△ABP绕点![]() 顺时针旋转60°得到△CBP′,连接
顺时针旋转60°得到△CBP′,连接![]() ,易证∠BP′P=__°,△____为等边三角形,
,易证∠BP′P=__°,△____为等边三角形,![]() ____
____![]() ,
,![]() ___°.
___°.
(2)点H为直线BP′上的一个动点,则![]() 的最小值为______;
的最小值为______;
(3)求![]() 长;
长;
拓展延伸
己知:点![]() 在正方形
在正方形![]() 内,点
内,点![]() 在平面内,
在平面内,![]() ,
,![]() .
.
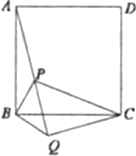
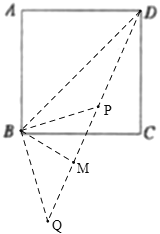
(4)在图中,连接PA、PC、PQ、QC,![]() ,若点
,若点![]() 、
、![]() 、
、![]() 在一条直线上,则
在一条直线上,则![]() ____.
____.
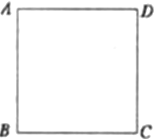
(5)若![]() ,连接
,连接![]() ,则______
,则______![]() ______;连接
______;连接![]() ,当
,当![]() 、
、![]() 、
、![]() 三点在同一条直线上时,△BDQ的面积为______.
三点在同一条直线上时,△BDQ的面积为______.
【答案】(1)60°,△BP′P,∠CP′P,150;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() ,
,![]() ,
,![]()
【解析】
(1)根据旋转的性质可得BP=BP′,∠PBP′=60°,AP=P′C,∠APB=∠BP′C,即可求出∠BP′P=60°,即可得△BP′P是等边三角形,根据勾股定理的逆定理可得∠CP′P=90°,即可得∠CP′B的度数,根据旋转性质可得∠APB=∠CP′B,即可得∠APB的度数;(2)过C作CH⊥BP′,交BP′的延长线于H,根据含30°角的直角三角形的性质求出CH的值即为最小值;(3)利用勾股定理可求出HP′的长,即可得BH的长,利用勾股定理求出BC的长进而可得答案;(4)由等腰直角三角形的性质可得∠BPQ=∠BQP=45°,PQ=![]() ,根据两锐角互余的关系可得∠CBQ=∠ABP,利用SAS可证明△ABP≌△CBQ,进而可得PA=CQ,∠BQC=∠BPA=135°,可得∠PQC=90°,利用勾股定理可求出PC的长,根据余弦的定义即可得答案;(5)连接BD,以B为圆心,1为半径画圆,交BD于P,交AB、BC于E、F,连接DF,则OP为最小值,根据正方形的性质及勾股定理求出DP、DF的值即可;当D、P、Q在同一条直线上时,过B作BM⊥DQ,根据等腰直角三角形的性质可得BM=QM=
,根据两锐角互余的关系可得∠CBQ=∠ABP,利用SAS可证明△ABP≌△CBQ,进而可得PA=CQ,∠BQC=∠BPA=135°,可得∠PQC=90°,利用勾股定理可求出PC的长,根据余弦的定义即可得答案;(5)连接BD,以B为圆心,1为半径画圆,交BD于P,交AB、BC于E、F,连接DF,则OP为最小值,根据正方形的性质及勾股定理求出DP、DF的值即可;当D、P、Q在同一条直线上时,过B作BM⊥DQ,根据等腰直角三角形的性质可得BM=QM=![]() PQ,利用勾股定理可求出DM的长,进而可得DQ的长,利用三角形面积公式即可得答案.
PQ,利用勾股定理可求出DM的长,进而可得DQ的长,利用三角形面积公式即可得答案.
(1)∵△ABP绕点![]() 顺时针旋转60°得到△CBP′,
顺时针旋转60°得到△CBP′,
∴BP=BP′=4,∠PBP′=60°,AP=P′C=2![]() ,∠APB=∠BP′C,
,∠APB=∠BP′C,
∴∠BP′P=60°,
∴△BP′P是等边三角形,
∴PP′=BP=4,
∵PC2=(2![]() )2=28,PP′2=42=16,P′C2=(2
)2=28,PP′2=42=16,P′C2=(2![]() )2=12,
)2=12,
∴PC2= PP′2+ P′C2,
∴△PP′C是直角三角形,∠CP′P=90°,
∴∠BP′C=∠CP′P+∠BP′P=90°+60°=150°,
∴∠APB=∠BP′C=150°,
故答案为:60°,△BP′P,∠CP′P,150°
(2)过C作CH⊥BP′,交BP′的延长线于H,
∵∠BP′C=150°,
∴∠P′HC=180°-150°=30°,
∴CH=![]() P′C=
P′C=![]() ,
,
故答案为:![]()
(3)∵CH=![]() ,P′C=PA=2
,P′C=PA=2![]() ,
,
∴P′H=![]() =3,
=3,
∴BC=![]() =
=![]() =2
=2![]() ,
,
∴AB=BC=2![]() .
.
(4)∵BP=BQ=1,BQ⊥BP,
∴∠BPQ=∠BQP=45°,PQ=![]() ,
,
∴∠APB=135°,
∵∠ABP+∠PBC=90°,∠CBQ+∠PBC=90°,
∴∠ABP=∠CBQ,
∵AB=BC,∠ABP=∠CBQ,BQ=BP,
∴△ABP≌△CBQ,
∴QC=AP=![]() ,∠BQC=∠APB=135°,
,∠BQC=∠APB=135°,
∴∠PQC=90°,
∴PC=![]() =
=![]() ,
,
∴cos∠PCQ=![]() =
=![]() =
=![]() ,
,
故答案为:![]()
(5)如图,连接BD,以B为圆心,1为半径画圆,交BD于P,交AB、BC于E、F,连接DF,
∵BP=1,
∴点P在以B为圆心,1为半径的圆上,
∴DP为最小值,
∵AB=AD=2,
∴BD=2![]() ,
,
∴DP=BD-BP=2![]() -1,
-1,
∵BF=1,CD=2,
∴DF=![]() ,
,
∵点P在正方形内,
∴2![]() -1≤DP<
-1≤DP<![]() ,
,
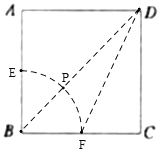
如图,当D、P、Q在同一条直线上时,过B作BM⊥DQ,
∵BQ=BP=1,BQ⊥BP,
∴BM=QM=![]() PQ=
PQ=![]() ,
,
∴DM=![]() =
=![]() ,
,
∴DQ=DM+QM=![]() +
+![]() =
=![]() ,
,
∴S△BDQ=![]() ×
×![]() ×
×![]() =
=![]() ,
,
故答案为:2![]() -1,
-1,![]() ,
,![]()


科目:初中数学 来源: 题型:
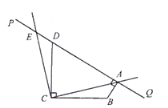
【题目】如图, ![]() ,且
,且![]() ,直线
,直线![]() 经过点
经过点![]() .设
.设![]() ,
,![]() 于点
于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
(1)当![]() 时,
时, ![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 的外心在其内部,直接写出
的外心在其内部,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
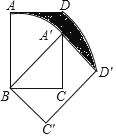
【题目】如图,在矩形ABCD中AB=![]() ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的边AB=6,BC=12,点P为矩形ABCD边上一点,连接AP,若线段AP、BD交点为点H,△PAB为等腰三角形,则AH的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
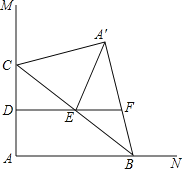
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
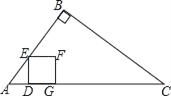
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在金融危机的影响下,国家采取扩大内需的政策,基建投资成为拉动内需最强有力的引擎.现金强公司中标一项工程,在甲、乙两地施工,其中甲地需推土机30台,乙地需推土机26台,公司在A、B两地分别库存推土机32台和24台,现从A地运一台到甲、乙两地的费用分别是400元和300元,从B地运一台到甲、乙两地的费用分别为200元和500元.若设从A地运往甲地![]() 台推土机,运甲、乙两地所需的这批推土机的总费用为
台推土机,运甲、乙两地所需的这批推土机的总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)公司应设计怎样的方案,能使运送这批推土机的总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com