
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌA(0ЃЌ4a)ЃЌB(3aЃЌ0)ЃЌЁїAOBЕФУцЛ§ЪЧ150ЃЎ
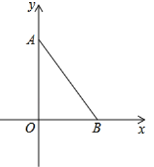
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЕуPЪЧЩфЯпABЩЯЕФвЛЕуЃЌЕуPЕФКсзјБъЮЊtЃЌСЌНгPOЃЌШєЁїPBOЕФУцЛ§ЮЊSЃЌЪдгУКЌгаtЕФЪНзгБэЪОSЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЕуPдкЕквЛЯѓЯоФкЃЌЧвSЁїPBOЃН126ЃЌЙ§PзїPEЁЭABЃЌНЛyжсгкЕуDЃЌНЛxжсгкЕуEЃЌЧвOBЃНODЃЌСЌНгAEЃЌMЮЊAEЩЯвЛЕуЃЌСЌНгOMНЛPEгкЕуNЃЌШєЁЯEMN+ЁЯABEЃН180ЁуЃЌЧѓЕуNЕФзјБъЃЎ![]()
ЁОД№АИЁПЃЈ1ЃЉA(0ЃЌ20)ЃЛЃЈ2ЃЉSЃН|Љ10t+150|ЃЛЃЈ3ЃЉ(Љ![]() ЃЌ
ЃЌ![]() )
)
ЁОНтЮіЁП
ЃЈ1ЃЉгЩШ§НЧаЮЕФУцЛ§ЙЋЪНПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуAзјБъЃЛ
ЃЈ2ЃЉЯШЧѓжБЯпABНтЮіЪНЃЌМДПЩЧѓЕуPзјБъЃЌгЩШ§НЧаЮУцЛ§ЙЋЪНПЩЧѓSгыtЕФЙиЯЕЃЛ
ЃЈ3ЃЉЯШЧѓГіPDНтЮіЪНЃЌЧѓГіЕуEзјБъЃЌПЩЕУEOЃНAOЃН20ЃЌЁЯAEOЃН45ЁуЃНЁЯEAOЃЌгЩШ§НЧаЮФкНЧКЭЖЈРэКЭгрНЧЕФаджЪПЩЧѓЁЯDNOЃНЁЯFONЃН45ЁуЃЌПЩЕУNFЃНFOЃЌгЩУцЛ§ЙЋЪНПЩЧѓFOЃН12ЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпAЃЈ0ЃЌ4aЃЉЃЌBЃЈ3aЃЌ0ЃЉЃЌ
ЁрAOЃН4aЃЌBOЃН3aЃЌaЃО0ЃЌ
ЁпЁїAOBЕФУцЛ§ЪЧ150ЃЎ
Ёр![]() AOЁСBOЃН150ЃЌ
AOЁСBOЃН150ЃЌ
Ёр6a2ЃН150ЃЌ
ЁрaЃН5ЃЌЃЈИКжЕВЛКЯЬтвтЩсШЅЃЉЃЌ
ЁрЕу AЃЈ0ЃЌ20ЃЉЃЛ
ЃЈ2ЃЉЁпaЃН5ЃЌ
ЁрAЃЈ0ЃЌ20ЃЉЃЌBЃЈ15ЃЌ0ЃЉЃЌ
ЩшжБЯпABНтЮіЪНЮЊЃКyЃНkx+20ЃЌ
Ёр0ЃН15k+20ЃЌ
ЁрkЃНЉ![]() ЃЌ
ЃЌ
ЁржБЯпABНтЮіЪНЮЊЃКyЃНЉ![]() x+20ЃЌ
x+20ЃЌ
ЁпЕуPЪЧЩфЯпABЩЯЕФвЛЕуЃЌ
ЁрЕуPЃЈtЃЌЉ![]() t+20ЃЉ
t+20ЃЉ
ЁпSЃНSЁїPOBЃН![]() ЁСOBЁС|yP|
ЁСOBЁС|yP|
ЁрSЃН![]() ЁС|Љ
ЁС|Љ![]() t+20|ЃН|Љ10t+150|ЃЌ
t+20|ЃН|Љ10t+150|ЃЌ
ЃЈ3ЃЉШчЭМ1ЃЌЙ§ЕуOзїOFЁЭDEЃЌ
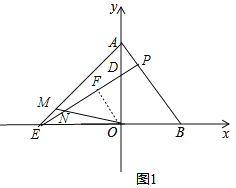
ЁпЕуPдкЕквЛЯѓЯоФкЃЌЧвSЁїPBOЃН126ЃЌ
Ёр126ЃНЉ10t+150
ЁрtЃН![]() ЃЌ
ЃЌ
ЁрЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁпOBЃНODЃН15ЃЌ
ЁрЕуDЃЈ0ЃЌ15ЃЉ
ЩшжБЯпDPНтЮіЪНЮЊЃКyЃНmx+15ЃЌ
Ёр![]() ЃН
ЃН![]() m+15
m+15
ЁрmЃН![]() ЃЌ
ЃЌ
ЁржБЯпPDНтЮіЪНЮЊЃКyЃН![]() x+15ЃЌ
x+15ЃЌ
ЁрЩшЕуNЃЈxЃЌ![]() x+15ЃЉ
x+15ЃЉ
ЁпжБЯпPDНЛxжсгкЕуEЃЌ
ЁрЕуEЃЈЉ20ЃЌ0ЃЉЃЌ
ЁрEOЃНAOЃН20ЃЌ
ЁрЁЯAEOЃН45ЁуЃНЁЯEAOЃЌ
ЁпЁЯDAP+ЁЯADPЃН90ЁуЃЌЁЯABO+ЁЯDAPЃН90ЁуЃЌ
ЁрЁЯADPЃНЁЯABOЃНЁЯNDOЃЌ
ЁпЁЯEMN+ЁЯABEЃН180ЁуЃЌЁЯEMN+ЁЯAMOЃН180ЁуЃЌ
ЁрЁЯAMOЃНЁЯABEЃНЁЯNDOЃЌ
ЁпЁЯAMO+ЁЯMAO+ЁЯAOMЃН180ЁуЃЌЁЯNDO+ЁЯDON+ЁЯDNOЃН180ЁуЃЌ
ЁрЁЯEAOЃНЁЯDNOЃН45ЁуЃЌЧвFOЁЭDEЃЌ
ЁрЁЯDNOЃНЁЯFONЃН45ЁуЃЌ
ЁрNFЃНFOЃЌ
ЁрNOЃН![]() FOЃЌ
FOЃЌ
гЩЙДЙЩЖЈРэПЩЕУЃКDEЃН![]() ЃН
ЃН![]() ЃН25ЃЌ
ЃН25ЃЌ
ЁпSЁїDEOЃН![]() DOЁСEOЃН
DOЁСEOЃН![]() ЁСDEЁСOF
ЁСDEЁСOF
ЁрOFЃН12ЃЌ
ЁрNOЃН12![]()
ЁрЃЈxЉ0ЃЉ2+ЃЈ![]() x+15Љ0ЃЉ2ЃН288ЃЌ
x+15Љ0ЃЉ2ЃН288ЃЌ
Ёрx1ЃНЉ![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрЕуNзјБъЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ


 аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
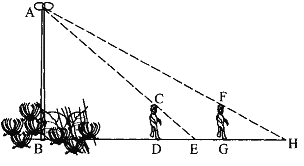
ЁОЬтФПЁПШчЭМЃЌЛЈДджагавЛТЗЕЦИЫAB. дкЕЦЙтЯТЃЌаЁУїдкDЕуДІЕФгАГЄDE=3УзЃЌбиBDЗНЯђаазпЕНДяGЕуЃЌDG=5УзЃЌетЪБаЁУїЕФгАГЄGHЃН5Уз. ШчЙћаЁУїЕФЩэИпЮЊ1.7УзЃЌЧѓТЗЕЦИЫABЕФИпЖШ(ОЋШЗЕН0.1Уз)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїBACжаЃЌЁЯBКЭЁЯCЕФЦНЗжЯпЯрНЛгкЕуFЃЌЙ§ЕуFзїDEЁЮBCНЛABгкЕуDЃЌНЛACгкЕуEЃЌШєBD=5ЃЌCE=4ЃЌдђЯпЖЮDEЕФГЄЮЊЃЈЁЁЁЁЃЉ
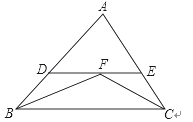
A. 9 B. 6 C. 5 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуOгызјБъдЕужиКЯЃЌAЁЂCЗжБ№дкзјБъжсЩЯЃЌЕуBЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌжБЯп![]() НЛABЃЌBCЗжБ№гкЕуMЃЌNЃЌЗДБШР§КЏЪ§
НЛABЃЌBCЗжБ№гкЕуMЃЌNЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§ЕуMЃЌNЃЎ
ЕФЭМЯѓОЙ§ЕуMЃЌNЃЎ

ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPдкyжсЩЯЃЌЧвЁїOPMЕФУцЛ§гыЫФБпаЮBMONЕФУцЛ§ЯрЕШЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
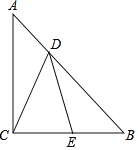
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌACЃНBCЃЌЁЯACBЃН90ЁуЃЌЕуDдкABЩЯЃЌЕуEдкBCЩЯЃЌЧвADЃНBEЃЌBDЃНACЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЃНED
ЃЈ2ЃЉжБНгаДГіЭМжаЫљгаЪЧЁЯACDЕФ2БЖЕФНЧЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіжНКаФкга![]() еХЭъШЋЯрЭЌЕФПЈЦЌЃЌЗжБ№БъКХЮЊ
еХЭъШЋЯрЭЌЕФПЈЦЌЃЌЗжБ№БъКХЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЫцЛњГщШЁвЛеХПЈЦЌКѓВЛЗХЛиЃЌдйЫцЛњГщШЁСэвЛеХПЈЦЌЃЎ
ЃЎЫцЛњГщШЁвЛеХПЈЦЌКѓВЛЗХЛиЃЌдйЫцЛњГщШЁСэвЛеХПЈЦЌЃЎ
ЃЈ1ЃЉгУСаОйЗЈЧѓЁАСНДЮГщГіПЈЦЌЕФБъКХЕШгк![]() ЁБЕФИХТЪЃЛ
ЁБЕФИХТЪЃЛ
ЃЈ2ЃЉаЁУїЭЌбЇСЌајзіСЫ![]() ДЮЪдбщЃЌет
ДЮЪдбщЃЌет![]() ДЮЪдбщУЛгавЛДЮГіЯжЁАСНДЮГщГіПЈЦЌЕФБъКХКЭЕШгк
ДЮЪдбщУЛгавЛДЮГіЯжЁАСНДЮГщГіПЈЦЌЕФБъКХКЭЕШгк![]() ЁБЃЎЫћЫЕЃЌЁАЕк
ЁБЃЎЫћЫЕЃЌЁАЕк![]() ДЮЪдбщЮввЛЖЈФмЙЛЁЎСНДЮГщГіПЈЦЌЕФБъКХКЭЕШгк
ДЮЪдбщЮввЛЖЈФмЙЛЁЎСНДЮГщГіПЈЦЌЕФБъКХКЭЕШгк![]() ЁЏЁБЃЎФуШЯЮЊЫћЫЕЕУЖдТ№ЃЌЮЊЪВУДЃП
ЁЏЁБЃЎФуШЯЮЊЫћЫЕЕУЖдТ№ЃЌЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
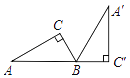
ЁОЬтФПЁПШчЭМЃЌRtЁїA'BC'ЪЧгЩRtЁїABCШЦBЕуЫГЪБеыа§зЊЖјЕУЃЌЧвЕуAЃЌBЃЌC'дкЭЌвЛЬѕжБЯпЩЯЃЌдкRtЁїABCжаЃЌШєЁЯC=90ЁуЃЌBC=2ЃЌAB=4ЃЌдђRtЁїABCа§зЊЕНRtЁїA'BC'ЫљЩЈЙ§ЕФУцЛ§ЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХвЦЖЏЛЅСЊЭјЕФПьЫйЗЂеЙЃЌЛљгкЛЅСЊЭјЕФЙВЯэЕЅГЕгІдЫЖјЩњЃЎЮЊСЫНтФГаЁЧјОгУёЪЙгУЙВЯэЕЅГЕЕФЧщПіЃЌФГбаОПаЁзщЫцЛњВЩЗУИУаЁЧјЕФ10ЮЛОгУёЃЌЕУЕНет10ЮЛОгУёвЛжмФкЪЙгУЙВЯэЕЅГЕЕФДЮЪ§ЗжБ№ЮЊЃК17ЃЌ12ЃЌ15ЃЌ20ЃЌ17ЃЌ0ЃЌ7ЃЌ26ЃЌ17ЃЌ9ЃЎ
ЃЈ1ЃЉетзщЪ§ОнЕФжаЮЛЪ§ЪЧЁЁ ЁЁЃЌжкЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉМЦЫует10ЮЛОгУёвЛжмФкЪЙгУЙВЯэЕЅГЕЕФЦНОљДЮЪ§ЃЛ
ЃЈ3ЃЉШєИУаЁЧјга200УћОгУёЃЌЪдЙРМЦИУаЁЧјОгУёвЛжмФкЪЙгУЙВЯэЕЅГЕЕФзмДЮЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЬьЭэЩЯЃЌаЁРіАяТшТшЧхЯДВшБЃЌШ§ИіВшБжЛгаЛЈЩЋВЛЭЌЃЌЦфжавЛИіЮоИЧЃЈШчЭМЃЉЃЌдкЧхЯДЙ§ГЬжаЃЌЭЛШЛЭЃЕчСЫЃЌаЁРіжЛКУУўКкЧхЯДЃЈдкУўКкЧхЯДжаЃЌФмЗжЧхБИЧгыВшБЃЉ
ЃЈ1ЃЉаЁРіУўКкЧхЯДЙ§ГЬжаЃЌдкШ§ИіВшБжаЫћЫцЪжФУЦ№СНИіЃЌдђетСНИіЖМЪєгкгаБИЧЕФВшБЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉаЁРіУўКкЧхЯДЭъВшБКЭБИЧКѓЃЌжЛКУАбБИЧгыВшБЫцЛњЕиДюХфдквЛЦ№ЃЌдђЛЈЩЋДюХфЭъШЋе§ШЗЕФИХТЪЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com