
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 为边
为边![]() 的中点,以
的中点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交腰
交腰![]() 于点
于点![]() ,射线
,射线![]() 交腰
交腰![]() 于点
于点![]() ,联结
,联结![]() .
.

(1)求证:![]() ;
;
(2)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的长;
的长;
(3)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据相似三角形的判定证出:![]() ,从而得出
,从而得出![]() ,再结合已知条件可得:
,再结合已知条件可得:![]() ,从而证出:
,从而证出:![]() .
.
(2)根据腰的情况分类讨论:①若BM=EM=3时,根据相似三角形的性质,可证出:FM=EF,CF=FM,从而证出:∠B=∠FMB,再根据平行线的判定即可得:MF∥AB,连接DM根据平行四边形的判定可得:四边形ABMD是平行四边形,从而证出:MD∥AB,故可判定此时D、F重合,从此得出EF=FM=FC=DC=6;②若BM=BE=3时,易证EF为梯形ABCD的中位线,从而求出EF;
(3)根据相似三角形的性质和已知条件可得:![]() ,过点
,过点![]() 作
作![]() ,过点A作
,过点A作![]() ,然后求出cosB,设
,然后求出cosB,设![]() ,则
,则![]() ,根据勾股定理:
,根据勾股定理:![]() ,根据BH+HM=BM即可求出BE.
,根据BH+HM=BM即可求出BE.
(1)在梯形![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
又![]() ,
,
![]() .
.
(2)∵![]() ,点
,点![]() 为边
为边![]() 的中点
的中点
∴BM=![]()
①若BM=EM=3时
∵![]() ,
,
∴![]() ,
,
∴FM=EF
∵![]()
∴![]()
∴CF=FM
∴∠C=∠FMB
∴∠B=∠FMB
∴MF∥AB
连接DM
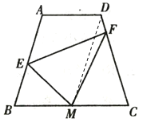
∵AD=BM=3,AD∥BM
∴四边形ABMD是平行四边形
∴MD∥AB
∴此时D、F重合
∴EF=FM=FC=DC=6;
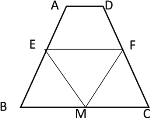
②若BM=BE=3时,
∴E为AB的中点
∵![]()
∴![]()
∴CF=CM=3
∴F为CD的中点
∴EF为梯形ABCD的中位线
∴EF=![]()
综上所述:![]() 或
或![]() .
.
(3)![]() ,
,![]() ,
,![]() ,
,
![]() .
.
过点![]() 作
作![]() ,过点A作
,过点A作![]()
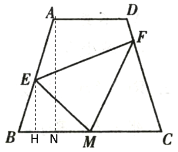
∴BN=![]()
∴cosB=![]()
设![]() ,
,
则![]() ,根据勾股定理:
,根据勾股定理:![]() ,
,
∵BH+HM=BM
∴![]() ,
,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(1)求m的值和反比例函数的表达式;
(2)观察图像,直接写出不等式2x+6-![]() >0的解集
>0的解集
(3)在反比例函数图像的第一象限上有一动点M,当S△BOM<S△BOD 时,直接写出点M纵坐标的的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
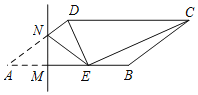
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
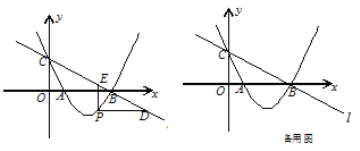
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售水果时,将A、B、C三种水果采用甲、乙、丙三种方式搭配装箱进行销售,毎箱的成本分别为箱中A、B、C三种水果的成本之和,箱子成本忽略不计.甲种方式每箱分别装A、B、C三种水果6kg、3kg、1kg,乙种方式每分別裳A、B、C三种水果2kg、6kg、2kg,甲每箱的总成本是每千克A成本的15倍,每箱甲的销售利润率为20%,每箱甲比每箱乙的售价低25%;丙每箱在成本上提高40%标价后打八折销售获利为每千克A成本的1.2倍,当销售甲、乙、丙三种方式的水果数量之比为2:1:5时,则销售的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
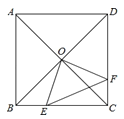
【题目】如图,正方形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 两点同时出发,以
两点同时出发,以![]() 的速度沿
的速度沿![]() ,
,![]() 运动,到点
运动,到点![]() ,
,![]() 时停止运动,设运动时间为
时停止运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A. B.
B.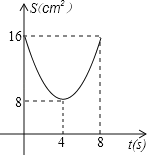 C.
C.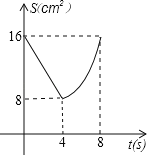 D.
D.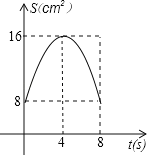
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com