【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点，叫格点，以格点为顶点的多边形叫格点多边形.设格点多边形的面积为
，它各边上格点的个数之和为
.
探究一：图中①—④的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数之和的对应关系如表：
多边形的序号 | ① | ② | ③ | ④ | … |
多边形的面积 | 2 | 2.5 | 3 | 4 | … |
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
与之间的关系式为：________.
探究二：图中⑤—⑧的格点多边形内部都只有2个格点，请你先完善下表格的空格部分（即分别计算出对应格点多边形的面积）：
多边形的序号 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多边形的面积 | … | ||||
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
与之间的关系式为：________.
猜想：当格点多边形内部有且只有
个格点时，与之间的关系式为：_______.
【答案】探究一：
；探究二：完整的表格信息见详解，
；猜想：
.
【解析】
探究一：通过观察可以看出多边形的面积等于各边上格点个数的一半，即；
探究二：用“切割法”将⑤—⑧中图形分割成几个三角形或者矩形即可求出其面积，
通过观察可以发现多边形的面积等于各边上格点的个数和的一半加1，即，
猜想：观察可发现⑤—⑧多边形内部都有2个格点，面积在探究一的基础上加1，结合探究一、二可得出解析式
探究一：当S=2时，x=4；当S=2.5时，x=5；…..通过观察多边形的面积等于各边上格点个数的一半，即；
探究二：表格填写如下
多边形的序号 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多边形的面积 | 3 | 3.5 | 4 | 5 | … |
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
通过观察可以发现多边形的面积等于各边上格点个数的一半再加1，即；
猜想：比较探究二与探究一，图形面积加1，图形内部格点个数加2，也就是多边形内部格点数每增加n个，面积就比原来多了n-1，故S与x的关系式为
.
科学实验活动册系列答案科目：初中数学 来源： 题型：
【题目】世界上大部分国家都使用摄氏温度(
)，但美国、英国等国家的天气预报仍然使用华氏温度(
).两种计量之间有如下对应：
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系？哪个是自变量？哪个是因变量？
(2)由上表可得：摄氏温度()每提高
度，华氏温度()提高_____度.
(3)摄氏温度
度时华氏温度为______度.
(4)华氏温度
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗？如果有，求出这个值.如果没有，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二孩子政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度，在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：
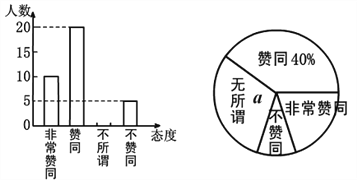
（1）在这次问卷调查中一共抽取了__________名学生，a=________%；
（2）请补全条形统计图；
（3）持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度；
（4）若该校有3000名学生，请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请认真观察如下图形：
当
时，长方形
分为2个直角三角形；
当
时，长方形分为8个直角三角形；
当
时，长方形分为18个直角三角形；
……
依此规律，第
个图形中，长方形被分成______个小直角三角形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料I：教材中我们学习了:若关于
的一元二次方程
的两根为
，根据这一性质，我们可以求出己知方程关于
的代数式的值．
问题解决:
（1）已知为方程
的两根，则
，
，那么
.(请你完成以上的填空)
阅读材料II：已知
，且
．求
的值．
解:由
可知
又
且，即
是方程
的两根．
问题解决:
（2）已知
且．求
的值；
，则
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题再现：
数形结合是一种重要的数学思想方法，借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如：利用图形的几何意义验证完全平方公式.
将一个边长为
的正方形的边长增加
，形成两个长方形和两个正方形，如图所示：这个图形的面积可以表示成：
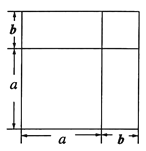
或
∴
这就验证了两数和的完全平方公式.
类比解决：
请你类比上述方法，利用图形的几何意义验证平方差公式.
（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明
？
如图所示，
表示1个1×1的正方形，即：
，
表示1个2×2的正方形，
与
恰好可以拼成1个2×2的正方形，因此：、、就可以表示2个2×2的正方形，即：
而、、、恰好可以拼成一个
的大正方形.
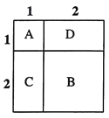
由此可得：
.
尝试解决：
请你类比上述推导过程，利用图形的几何意义确定：
_______.（要求写出结论并构造图形写出推证过程）.
问题拓广：
请用上面的表示几何图形面积的方法探究：
_______.（直接写出结论即可，不必写出解题过程）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是矩形，对角线AC的垂直平分线EF交AC于O，分别交BC、AD于点E、F．
（1）求证：四边形AECF是菱形；
（2）若AB=4，BC=8，求EC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车专卖店销售A，B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元.
（1）求每辆A型车和B型车的售价各为多少万元？
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“龟兔赛跑”的故事同学们非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列的问题：
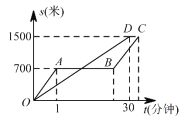
（1）折线OABC表示赛跑过程中__________（填“兔子”或“乌龟”）的路程与时间的关系，赛跑的全程是_________米；
（2）乌龟用了多少分钟追上正在睡觉的兔子？
（3）兔子醒来，以400米/分的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你计算兔子中间睡觉用了多少分钟？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
