
在四边形 中,
中,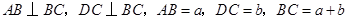 ,且
,且 .取
.取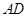 的中点
的中点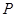 ,连结
,连结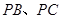 .
.

(1)试判断三角形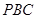 的形状;
的形状;
(2)在线段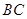 上,是否存在点
上,是否存在点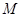 ,使
,使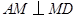 .若存在,请求出
.若存在,请求出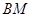 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)等腰直角三角形(2)存在,当 时,有一点
时,有一点 ,
, ;当
;当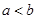 时,有两点
时,有两点 ,
,
【解析】解:(1)在四边形 中,
中,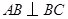 ,
, ,
,
 四边形
四边形 为直角梯形(或矩形).
为直角梯形(或矩形).
过点 作
作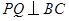 ,垂足为
,垂足为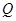 ,
, ,
,

又点 是
是 的中点,
的中点, 点
点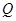 是
是 的中点,
的中点,
又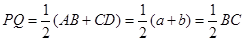 ,
,
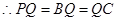 ,
,
 与
与 是全等的等腰直角三角形,
是全等的等腰直角三角形,
 ,
,
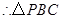 是等腰直角三角形.
是等腰直角三角形.
(2)存在点 使
使 .
.
以 为直径,
为直径, 为圆心作圆
为圆心作圆 .
.
当 时,四边形
时,四边形 为矩形,
为矩形, ,
,
圆 与
与 相切于点
相切于点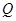 ,此时,
,此时, 点与
点与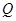 点重合,存在点
点重合,存在点 ,使得
,使得 ,
,
此时 .
.
当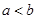 时,四边形
时,四边形 为直角梯形,
为直角梯形,
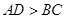 ,
, ,圆心
,圆心 到
到 的距离
的距离 小于圆
小于圆 的半径,圆
的半径,圆 与
与 相交,
相交, 上存在两点
上存在两点 ,使
,使 ,
,
过点 作
作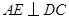 ,在
,在 中,
中, ,
,
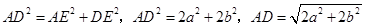
连结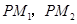 ,则
,则 ,
,
在直角三角形 中,
中, ,
,
 .
.
同理可得: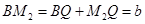 .
.
综上所述,在线段 上存在点
上存在点 ,使
,使 .
.
当 时,有一点
时,有一点 ,
, ;当
;当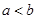 时,有两点
时,有两点 ,
, .
.
根据已知条件,得到四边形ABCD为直角梯形或矩形.
(1)过点P作PQ⊥BC,易证PQ=BQ=QC,则△PQB与△PQC是全等的等腰直角三角形,因而△PBC是等腰直角三角形.
(2)判断在线段BC上,是否存在点M,使AM⊥MD,利用相似三角形的性质与判定得出即可.


科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2009年初中毕业升学考试(山东潍坊卷)数学(带解析) 题型:解答题
在四边形 中,
中,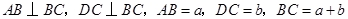 ,且
,且 .取
.取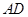 的中点
的中点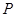 ,连结
,连结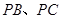 .
.
(1)试判断三角形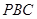 的形状;
的形状;
(2)在线段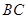 上,是否存在点
上,是否存在点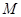 ,使
,使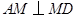 .若存在,请求出
.若存在,请求出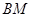 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市东城区初三第一学期期末统一测试数学试卷(解析版) 题型:解答题
阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出 的值.
的值.
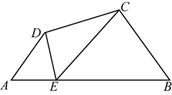
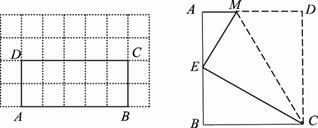
图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com