【题目】(1)化简:
(2)计算:
；
(3)化简:
；
(4)已知
求代数式
的值；
(5)已知
求代数式
的值.
【答案】（1）2xy-y2；（2）1；（3）-11a6；（4）6；（5）13.
【解析】
（1）原式第一项利用单项式乘以多项式的运算法则进行计算，第二项运用完全平方公式进行计算，去括号合并同类项即可得到结果；
（2）原式第二项2010变成2009+1，2008变成2009-1，利用平方差公式化简，去括号合并即可得到结果；
（3）原式先利用积的乘方和幂的乘方运算法则进行计算，合并同类项即可得到结果；
（4）先根据整式的混合运算顺序和运算法则进行化简，再将
即
整体代入即可；
（5）先根据多项式除以单项式的法则计算原式，再将n的值代入计算即可得结果.
（1）
=
=
；
（2）
=
=
=1；
（3）
=
=
；
（4）
=
=
当即时，
原式=3（
）+9
=-3+9
=6；
（5）
=2n2-2n+1
当n=-2时，
原式=
=8+4+1
=13.
科目：初中数学 来源： 题型：
【题目】已知函数
.
（1）指出函数图象的开口方向是 ，对称轴是 ，顶点坐标为 ；
（2）当x 时，y随x的增大而减小；
（3）怎样移动抛物线
就可以得到抛物线.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下说法合理的是：（ ）
A. “打开电视，正在播放新闻节日”是必然事件
B. “抛一枚硬币，正面朝上的概率为
”表示每抛两次就有一次正面朝上
C. “抛掷一枚均匀的骰子，出现点数6的概率是
”表示随着抛掷次数的增加“出现点数6”这一事件发生的频率稳定在附近
D. 为了解某品牌火腿的质量，选择全面检测
查看答案和解析>>
科目：初中数学 来源： 题型：
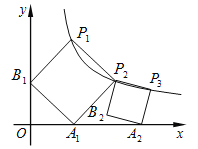
【题目】如图，正方形
的顶点
、
在反比例函数
的图象上，顶点
、
分别在
轴、
轴的正半轴上，再在其右侧作正方形
，顶点
在反比例函数的图象上，顶点
在轴的正半轴上，则点的坐标为____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．
（1）求证：△ABC≌△ADE；
（2）求∠FAE的度数；
（3）求证：CD=2BF+DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
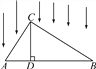
【题目】如图所示，△ABC被平行光线照射，CD⊥AB于D，AB在投影面上．
(1)指出图中AC的投影是什么？CD与BC的投影呢？
(2)探究：当△ABC为直角三角形(∠ACB＝90°)时，易得AC2＝AD·AB，此时有如下结论：直角三角形一直角边的平方等于它在斜边射影与斜边的乘积，这一结论我们称为射影定理．通过上述结论的推理，请证明以下两个结论．
①BC2＝BD·AB；②CD2＝AD·BD.
查看答案和解析>>
科目：初中数学 来源： 题型：
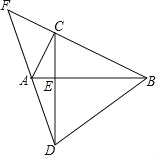
【题目】如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于E，CD＝AB，DA、BC延长线交于F．
（1）若AC＝12，∠ABC＝30°，求DE的长；
（2）若BC＝2AC，求证：DA＝
FC．
查看答案和解析>>
科目：初中数学 来源： 题型：
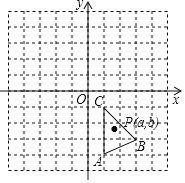
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，-4），B（3，-3），C（1，-1）．
（1）将△ABC先向上平移5个单位，再向左平移3个单位，画出平移后得到的△A1B1C1；
（2）写出△A1B1C1各顶点的坐标；
（3）若△ABC内有一点P（a，b），请写出平移后得到的对应点P1的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
