
【题目】如图,![]() 是边长为6的等边三角形,
是边长为6的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
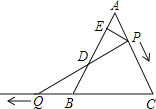
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由.
【答案】(1)2;(2)不变,DE=3为定值.
【解析】
(1)过P作PF∥QC,证明△DBQ≌△DFP,根据全等三角形的性质计算即可;
(2)根据等边三角形的性质、直角三角形的性质解答.
(1)解:过P作PF∥QC,
则△AFP是等边三角形,
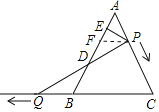
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中, ,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30°,
∴BD=DF=FA=![]() AB=2,
AB=2,
∴AP=2;
(2)解:由(1)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=3为定值,即DE的长不变.
AB=3为定值,即DE的长不变.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列材料:
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法.
如:ax+by+bx+ay=(ax+bx)+(ay+by)
=x(a+b)+y(a+b)
=(a+b)(x+y)
2xy+y2﹣1+x2
=x2+2xy+y2﹣1
=(x+y)2﹣1
=(x+y+1)(x+y﹣1)
(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:
x2+2x﹣3
=x2+2x+1﹣4
=(x+1)2﹣22
=(x+1+2)(x+1﹣2)
=(x+3)(x﹣1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式: ![]()
(2)分解因式:x2﹣6x﹣7;
(3)分解因式: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图①,在
如图①,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,
,![]() ,求证:
,求证:![]() 是
是![]() 的完美分割线;
的完美分割线;
![]() 如图②,在
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
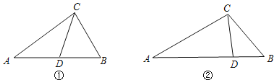
查看答案和解析>>
科目:初中数学 来源: 题型:
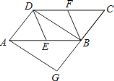
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
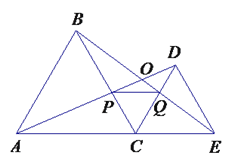
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是( )
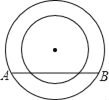
A. 4<AB<5 B. 6<AB<10 C. 6≤AB<10 D. 6<AB≤10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com