
【题目】如图,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线
点,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于另一点
轴交于另一点![]() .
.
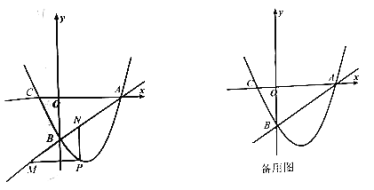
(1)求直线及抛物线的解析式;
(2)点![]() 是抛物线上一动点,当点
是抛物线上一动点,当点![]() 在直线
在直线![]() 下方的抛物线上运动时,过点
下方的抛物线上运动时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)在(2)的条件下,当![]() 的值最大时,将
的值最大时,将![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 落在
落在![]() 轴上时,直接写出此时点
轴上时,直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,最大值为6;(3)点
有最大值,最大值为6;(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)把点![]() 代入直线
代入直线![]() ,求出
,求出![]() 的值,即可求出直线的解析式,根据直线解析式求出点B的坐标,利用待定系数法即可求出抛物线的解析式;
的值,即可求出直线的解析式,根据直线解析式求出点B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)设![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,表示出
,表示出![]() ,
,![]() ,计算
,计算![]() 根据二次函数的性质进行求解即可.
根据二次函数的性质进行求解即可.
(3)当![]() 最大时
最大时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,分两种情况进行讨论即可.
,分两种情况进行讨论即可.
(1)把点![]() 代入直线
代入直线![]() 得:
得:![]() ,
,
∴![]() ,
,
∴![]() .
.
把点![]() ,
,![]() ,
,![]() 代入
代入![]() 得:
得:
 ,∴
,∴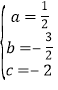 ,
,
∴![]() .
.
(2)设![]() 点坐标为
点坐标为![]() ,∵
,∵![]() 轴,
轴,![]() 轴,
轴,![]() 、
、![]() 在直线
在直线![]() 上,
上,
∴![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值,最大值为6.
有最大值,最大值为6.
(3)当![]() 最大时
最大时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,
∵![]() 为直角三角形,且
为直角三角形,且![]() ,
,![]() ,
,![]() ,
,
如图一:过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,可得:
,可得:![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
如图二:同理可得:![]() ,
,
∴![]() ,
,
设![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求此反比例函数的解析式;
(2)问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?
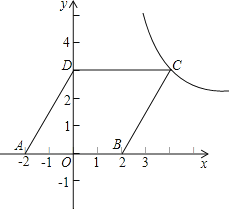
查看答案和解析>>
科目:初中数学 来源: 题型:
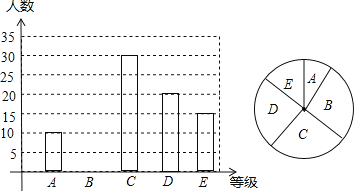
【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
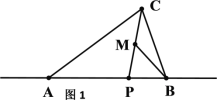
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
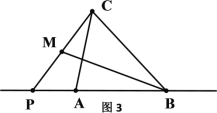
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
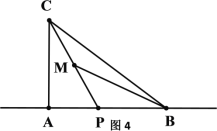
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
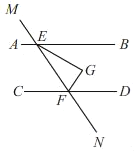
A. 20°B. 25°C. 35°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
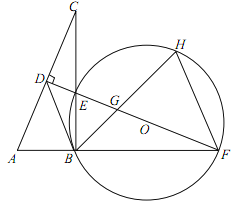
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
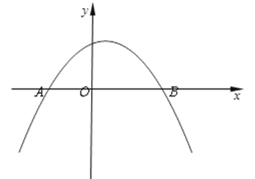
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com