
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
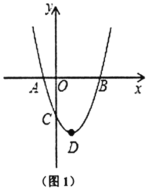
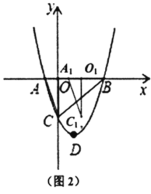
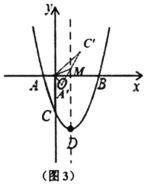
ЃЈ1ЃЉХзЮяЯпЖЅЕу![]() ЕФзјБъЮЊ________ЃЛ
ЕФзјБъЮЊ________ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎНЋ
ЃЎНЋ![]() би
би![]() жсЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвЦНвЦЕУЕН
жсЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвЦНвЦЕУЕН![]() ЃЌдЫЖЏЪБМфЮЊ
ЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎЕБ
УыЃЎЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() гы
гы![]() жиЕўУцЛ§
жиЕўУцЛ§![]() гы
гы![]() ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГі
ЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ3жаЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊвЛЖЈЕФНЧЖШ
ЫГЪБеыа§зЊвЛЖЈЕФНЧЖШ![]() ЕУЕН
ЕУЕН![]() ЃЌБп
ЃЌБп![]() гыХзЮяЯпЕФЖдГЦжсНЛгкЕу
гыХзЮяЯпЕФЖдГЦжсНЛгкЕу![]() ЃЎдка§зЊЙ§ГЬжаЃЌЪЧЗёДцдквЛЕу
ЃЎдка§зЊЙ§ГЬжаЃЌЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФЕу
ЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ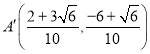 Лђ
Лђ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAКЭЕуBЕФзјБъПЩЕУЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЌШЛКѓНЋЦфЛЏЮЊЖЅЕуЪНМДПЩЕУГіНсТлЃЛ
ЃЌШЛКѓНЋЦфЛЏЮЊЖЅЕуЪНМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнtЕФШЁжЕЗЖЮЇЗжРрЬжТлЃЌШЛКѓРћгУ![]() ЕФУцЛ§МѕШЅЦфгрИїШ§НЧаЮЕФУцЛ§МДПЩЗжБ№ЧѓГі
ЕФУцЛ§МѕШЅЦфгрИїШ§НЧаЮЕФУцЛ§МДПЩЗжБ№ЧѓГі![]() гы
гы![]() ЕФКЏЪ§НтЮіЪНЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪЧѓзюжЕМДПЩЃЛ
ЕФКЏЪ§НтЮіЪНЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪЧѓзюжЕМДПЩЃЛ
ЃЈ3ЃЉШчЭМЃЌЩш![]() ЮЊ
ЮЊ![]() ЃЌЕуMЮЊЃЈ1ЃЌmЃЉЃЌЙ§ЕуAЁфзїAЁфPЁЭyжсгкP,Й§ЕуCЁфQЁЭyжсгкQЃЌвзжЄЁїAЁфPOЁзЁїOQCЁфЃЌСаГіБШР§ЪНМДПЩЧѓГіЕуCЁфЕФзјБъЃЌИљОнШ§НЧаЮЭтНЧЕФаджЪКЭЕШНЧЖдЕШБпПЩжЄ
ЃЌЕуMЮЊЃЈ1ЃЌmЃЉЃЌЙ§ЕуAЁфзїAЁфPЁЭyжсгкP,Й§ЕуCЁфQЁЭyжсгкQЃЌвзжЄЁїAЁфPOЁзЁїOQCЁфЃЌСаГіБШР§ЪНМДПЩЧѓГіЕуCЁфЕФзјБъЃЌИљОнШ§НЧаЮЭтНЧЕФаджЪКЭЕШНЧЖдЕШБпПЩжЄ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌРћгУЙДЙЩЖЈРэЧѓГіЕуMЕФзјБъМДПЩЧѓГіЕуaКЭbЃЌДгЖјЧѓГіЕуAЁфЕФзјБъЃЎ
ЕФжаЕуЃЌРћгУЙДЙЩЖЈРэЧѓГіЕуMЕФзјБъМДПЩЧѓГіЕуaКЭbЃЌДгЖјЧѓГіЕуAЁфЕФзјБъЃЎ
ЃЈ1ЃЉНтЃКгЩвбжЊХзЮяЯпгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]()
Ёр![]() ЃЌ
ЃЌ
ЁрЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉНтЃКЕБx=0ЪБЃЌy=-3
ЫљвдЕуCЕФзјБъЮЊЃЈ0ЃЌ-3ЃЉ
ЂйШчЭМЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ
![]()
![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЛ
ЃЛ
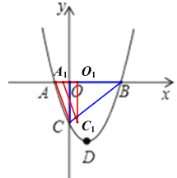
ЂкШчЭМЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЛ
ЃЛ
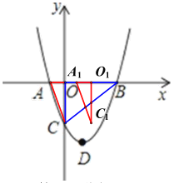
Ёп![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉНтЃКШчЭМЃЌЩш![]() ЮЊ
ЮЊ![]() ЃЌЕуMЮЊЃЈ1ЃЌmЃЉЃЌЙ§ЕуAЁфзїAЁфPЁЭyжсгкP,Й§ЕуCЁфQЁЭyжсгкQЃЌвзжЄЁїAЁфPOЁзЁїOQCЁф
ЃЌЕуMЮЊЃЈ1ЃЌmЃЉЃЌЙ§ЕуAЁфзїAЁфPЁЭyжсгкP,Й§ЕуCЁфQЁЭyжсгкQЃЌвзжЄЁїAЁфPOЁзЁїOQCЁф
Ёр![]()
ПЩЕУ![]() ЃЎ
ЃЎ
а§зЊЙ§ГЬжаЃЌШєДцдквЛЕу![]() ЪЙЕУ
ЪЙЕУ![]() ЃЌдђ
ЃЌдђ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]()
НтЕУЃКm=![]()
Ёр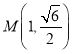 Лђ
Лђ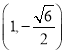
Ёр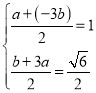 Лђ
Лђ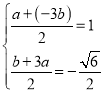
НтЕУЃК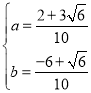 Лђ
Лђ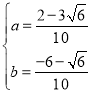
Ёр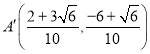 Лђ
Лђ ЃЎ
ЃЎ
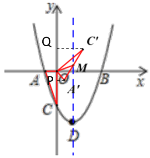



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
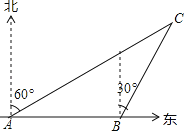
ЁОЬтФПЁПШчЭМЃЌвЛЫвгцДЌвд60КЃРяУПаЁЪБЕФЫйЖШЯђе§ЖЋЗНЯђКНааЃЎдкAДІВтЕУЕЦЫўCдкББЦЋЖЋ60ЁуЗНЯђЩЯЃЛМЬајКНаа1аЁЪБЕНДяBДІЃЌДЫЪБВтЕУЕЦЫўCдкББЦЋЖЋ30ЁуЗНЯђЩЯЃЎвбжЊдкЕЦЫўCжмЮЇ50КЃРяЗЖЮЇФкгаАЕНИЃЌЮЪетЫвгцДЌМЬајЯђЖЋКНаагаЮоДЅНИЕФЮЃЯеЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
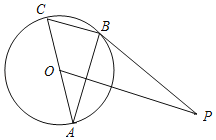
ЁОЬтФПЁПШчЭМЃЌACЪЧЁбOЕФжБОЖЃЌBCЪЧЁбOЕФЯвЃЌЕуPЪЧЁбOЭтвЛЕуЃЌСЌНгPBЁЂABЃЌЁЯPBAЃНЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКPBЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгOPЃЌШєOPЁЮBCЃЌЧвOPЃН4ЃЌЁбOЕФАыОЖЮЊ![]() ЃЌЧѓBCЕФГЄЃЎ
ЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЭЦНјШЋПЦдФЖСЃЌХрг§ЪБДњаТШЫЁБЃЎФГбЇаЃЮЊСЫИќКУЕиПЊеЙбЇЩњЖСЪщЛюЖЏЃЌЫцЛњЕїВщСЫОХФъМЖ50УћбЇЩњзюНќвЛжмЕФЖСЪщЪБМфЃЌЭГМЦЪ§ОнШчЯТБэЃК
ЪБМфЃЈаЁЪБЃЉ | 6 | 7 | 8 | 9 | 10 |
ШЫЪ§ | 5 | 8 | 12 | 15 | 10 |
ЃЈ1ЃЉИљОнЩЯЪіБэИёВЙШЋЯТУцЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉаДГіет50УћбЇЩњЖСЪщЪБМфЕФжкЪ§ЁЂжаЮЛЪ§ЁЂЦНОљЪ§ЃЛ
ЃЈ3ЃЉШєИУаЃга1000УћбЇЩњЃЌЧѓзюНќвЛжмЕФЖСЪщЪБМфВЛЩйгк7аЁЪБЕФШЫЪ§ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎНЋОиаЮби
ЃЎНЋОиаЮби![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпжаЕу
БпжаЕу![]() ДІЃЌЕу
ДІЃЌЕу![]() Тфдк
Тфдк![]() ДІЃЎСЌНг
ДІЃЎСЌНг![]() ЃЌвдОиаЮЖдГЦжааФ
ЃЌвдОиаЮЖдГЦжааФ![]() ЮЊдВаФЕФдВгы
ЮЊдВаФЕФдВгы![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ЃЌдђдВЕФАыОЖЮЊ________ЃЎ
ЃЌдђдВЕФАыОЖЮЊ________ЃЎ
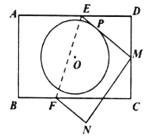
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
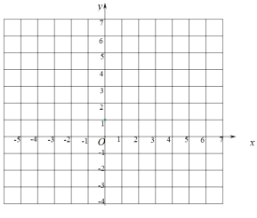
ЃЈ1ЃЉИљОнИјЖЈЕФЬѕМўЃЌдђ![]() _________ЃЌ
_________ЃЌ![]() ____________ЃЎ
____________ЃЎ
ЃЈ2ЃЉдкИјГіЕФЦНУцжБНЧзјБъЯЕжаЃЌЛГіКЏЪ§ЭМЯёЃЛ
ЃЈ3ЃЉЂйНсКЯЫљЛЕФЭМЯёЃЌжБНгаДГіЗНГЬ![]() ЕФНтЃЌНтЮЊ________________ЃЎЃЈОЋШЗЕНЪЎЗжЮЛЃЉ
ЕФНтЃЌНтЮЊ________________ЃЎЃЈОЋШЗЕНЪЎЗжЮЛЃЉ
ЂкШєвЛДЮКЏЪ§![]() ЕФЭМЯёгы
ЕФЭМЯёгы![]() ЕФЭМЯёгаЧвжЛгаШ§ИіНЛЕуЃЌдђ
ЕФЭМЯёгаЧвжЛгаШ§ИіНЛЕуЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
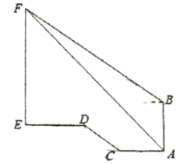
ЁОЬтФПЁПШчЭМЃЌЩШаЮAOBЕФдВаФНЧЮЊжБНЧЃЌБпГЄЮЊ1ЕФе§ЗНаЮODCFЕФЖЅЕуFЃЌDЃЌCЗжБ№дкOAЃЌOBЃЌ![]() ЩЯЃЌЙ§ЕуBзїBEЁЭFCЃЌНЛFCЕФбгГЄЯпгкЕуEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЕШгк__ЃЎ
ЩЯЃЌЙ§ЕуBзїBEЁЭFCЃЌНЛFCЕФбгГЄЯпгкЕуEЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЕШгк__ЃЎ
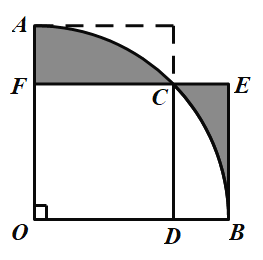
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃФГЪ§бЇаЫШЄаЁзщЯыВтбЇаЃЦьИЫИпЖШШчЭМЃЌУїУїдкЕОЯудАвЛТЅ![]() ЕуВтЕУЦьИЫЖЅЕу
ЕуВтЕУЦьИЫЖЅЕу![]() біНЧЮЊ
біНЧЮЊ![]() ЃЌдкЕОЯудАЖўТЅ
ЃЌдкЕОЯудАЖўТЅ![]() ЕуВтЕУЕу
ЕуВтЕУЕу![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЎУїУїДг
ЃЎУїУїДг![]() ЕуГЏЦьИЫЗНЯђВНаа
ЕуГЏЦьИЫЗНЯђВНаа![]() УзЕН
УзЕН![]() ЕуЃЌбиЦТЖШ
ЕуЃЌбиЦТЖШ![]() ЕФЬЈНззпЕНЕу
ЕФЬЈНззпЕНЕу![]() ЃЌдйЯђЧАзп
ЃЌдйЯђЧАзп![]() УзЕНЦьИЫЕзВП
УзЕНЦьИЫЕзВП![]() ЃЌвбжЊЕОЯудА
ЃЌвбжЊЕОЯудА![]() ИпЖШЮЊ
ИпЖШЮЊ![]() УзЃЌдђЦьИЫ
УзЃЌдђЦьИЫ![]() ЕФИпЖШдМЮЊЃЈ ЃЉЃЈВЮПМЪ§ОнЃК
ЕФИпЖШдМЮЊЃЈ ЃЉЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
A.![]() УзB.
УзB.![]() УзC.
УзC.![]() УзD.
УзD.![]() Уз
Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
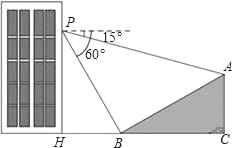
ЁОЬтФПЁПШчЭМЃЌаЁУїдкДѓТЅ30УзИпЃЈМДPHЃН30УзЃЉЕФДАПкPДІНјааЙлВтЃЌВтЕУЩНЦТЩЯAДІЕФИЉНЧЁЯAPQЮЊ15ЁуЃЌЩННХBДІЕФИЉНЧЁЯBPQЮЊ60ЁуЃЌвбжЊИУЩНЦТЕФЦТЖШiЃЈМДtanЁЯABCЃЉЮЊ1ЃК![]() ЃЌЕуPЃЌHЃЌBЃЌCЃЌAдкЭЌвЛИіЦНУцЩЯЃЌЕуHЁЂBЁЂCдкЭЌвЛЬѕжБЯпЩЯЃЌЧвPHAHCЃЎ
ЃЌЕуPЃЌHЃЌBЃЌCЃЌAдкЭЌвЛИіЦНУцЩЯЃЌЕуHЁЂBЁЂCдкЭЌвЛЬѕжБЯпЩЯЃЌЧвPHAHCЃЎ
ЃЈ1ЃЉЧѓГіЩНЦТЦТНЧЃЈЁЯABCЃЉЕФДѓаЁЃЛ
ЃЈ2ЃЉЧѓAЁЂBСНЕуМфЕФОрРыЃЈНсЙћОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃК![]() Ёж1.732ЃЉЃЎ
Ёж1.732ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com