
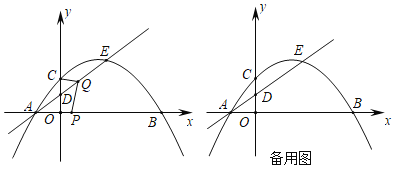
【题目】如图,在平面直角坐标系中,抛物线y=ax2+x+c与直线![]() 交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,
交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,![]() ),直线
),直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求点D的坐标和抛物线y=ax2+x+c的函数表达式;
(2)动点P从点B出发,沿x轴以每秒2个单位长度的速度向点A运动,动点Q从点A出发沿射线AE以每秒1个单位长度的速度向点E运动,当点P到达点A时,点P、Q同时停止运动.设运动时间为t秒,连接AC、CQ、PQ.
①当△APQ是以AP为底边的等腰三角形时,求t的值;
②在点P、Q运动过程中,△ACQ的面积记为S1,△APQ的面积记为S2,S=S1+S2,当S=![]() 时,请直接写出t的值.
时,请直接写出t的值.
【答案】(1)抛物线的函数表达式为![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据题意首先求出A、D的坐标,再利用待定系数法即可解决问题;
(2)①如图1,过点Q作QF⊥AP于点F,则AF=PF=![]() AP=
AP=![]() (5﹣2t),AQ=t,证得OD∥QF,得出
(5﹣2t),AQ=t,证得OD∥QF,得出![]() ,可求出t的值;
,可求出t的值;
②如图2,过点C作CM⊥AQ于点M,过点Q作QN⊥x轴于点N,证明△AOD∽△CMD,求出CM,则S1可用t表示,证明△AOD∽△AQN,求出QN,则S2可用t表示,则可得出t的方程,解方程即可得出答案.
解:(1)∵直线![]() 与y轴交于点D,
与y轴交于点D,
∴x=0时,y=![]() ,
,
∴D(0,![]() ),
),
∵直线![]() 与x轴交于点A,
与x轴交于点A,
∴y=0时,![]() =0,
=0,
∴x=﹣1,
∴A(﹣1,0),
∵抛物线y=ax2+x+c经过点A(﹣1,0),C(0,![]() ),
),
∴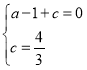 ,
,
解得: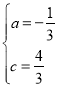 ,
,
∴抛物线的函数表达式为![]() ;
;
(2)①如图1,过点Q作QF⊥AP于点F,
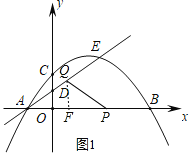
若AQ=PQ,则AF=PF=![]() AP=
AP=![]() (5﹣2t),AQ=t,
(5﹣2t),AQ=t,
∵OD⊥AP,QF⊥AP,
∴OD∥QF,
∴![]() ,
,
∵D(0,![]() ),A(﹣1,0),
),A(﹣1,0),
∴OD=![]() ,AO=1,
,AO=1,
∴AD=![]() =
=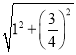 =
=![]() ,
,
∴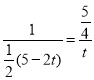 ,
,
解得:t=![]() .
.
∴t=![]() 时,△APQ是以AP为底边的等腰三角形.
时,△APQ是以AP为底边的等腰三角形.
②如图2,过点C作CM⊥AQ于点M,过点Q作QN⊥x轴于点N,
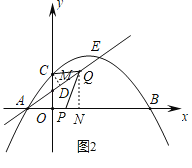
∵∠ADO=∠CDM,∠AOD=∠CMD=90°,
∴△AOD∽△CMD,
∴![]() ,
,
∵CD=OC﹣OD=![]() ,AD=
,AD=![]() ,OA=1,
,OA=1,
∴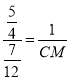 ,
,
∴CM=![]() ,
,
∴S△ACQ=S1=![]() AQ×CM=
AQ×CM=![]() =
=![]() ,
,
∵OD⊥x轴,QN⊥x轴,
∴OD∥QN,
∴△AOD∽△AQN,
∴![]() ,
,
∴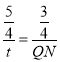 ,
,
∴QN=![]() t,
t,
∴S△APQ=S2=![]() AP×QN=
AP×QN=![]() =
=![]() ,
,
∵S1+S2=![]() ,
,
∴![]() ,
,
∴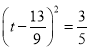 ,
,
解得:t=![]() .
.
即当S=![]() 时,t的值为
时,t的值为![]() .
.


科目:初中数学 来源: 题型:
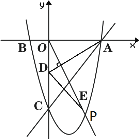
【题目】如图,抛物线![]() 经过点A(3,0),B(
经过点A(3,0),B(![]() ,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
(1)求抛物线解析式;
(2)点D是线段OC的中点,OP⊥AD,点E是射线OP上一点,OE=AD,求DE的长;
(3)连接CP,AP,是否存在点P,使得OP平分四边形ABCP的面积?若存在,求点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点P为⊙O 外一点,PA、PB是⊙O的切线,切点分别是A、B,连接OP交AB于点C,交⊙O于点D,若PA=3cm, ∠APB=60°,则下列结论正确的有( )
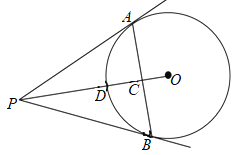
①AB⊥OP;②AC2=PC·OC;③若连接AD,BD,则∠ADB=120°;④PA,PB与劣弧AB围成的图形的面积是![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区新建成的住宅楼主体工程已经竣工,只剩下楼体外表需贴瓷砖,已知楼体外表的面积为![]() .
.
(1)写出每块瓷砖的面积![]() 与所需的瓷砖块数
与所需的瓷砖块数![]() (块)之间的函数关系式;
(块)之间的函数关系式;
(2)为了使住宅楼的外观更漂亮,开发商决定采用灰、白、蓝三种颜色的瓷砖,每块瓷砖的面积都是![]() ,灰、白、蓝瓷砖使用比例是
,灰、白、蓝瓷砖使用比例是![]() ,则需要三种瓷砖各多少块?
,则需要三种瓷砖各多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好“营造清洁生活环境”活动的宣传,对本校学生进行了有关知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
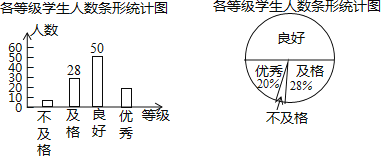
(1)求抽取的学生总人数;
(2)抽取的学生中,等级为“优秀”的人数为 人;扇形统计图中等级为“不合格”部分的圆心角的度数为 °;
(3)补全条形统计图;
(4)若该校有学生3500人,请根据以上统计结果估计成绩等级为“优秀”和“良好”的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
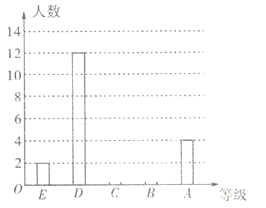
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
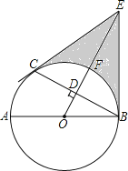
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF = 2,BC = ![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
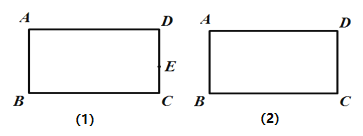
【题目】如图,四边形 ABCD 为矩形.
(1)如图1,E为CD上一定点,在AD上找一点F,使得矩形沿着EF折叠后,点D落在 BC边上(尺规作图,保留作图痕迹);
(2)如图2,在AD和CD边上分别找点M,N,使得矩形沿着MN折叠后BC的对应边B' C'恰好经过点D,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);
(3)在(2)的条件下,若AB=2,BC=4,则CN= .
查看答案和解析>>
科目:初中数学 来源: 题型:
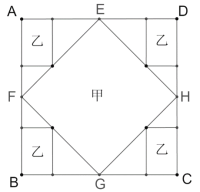
【题目】为了增加学校绿化,学校计划建造一块长为![]() 的正方形花坛
的正方形花坛![]() ,分别取四边中点
,分别取四边中点![]() ,构成四边形
,构成四边形![]() ,并计划用“两花一草”来装饰,四边形
,并计划用“两花一草”来装饰,四边形![]() 部分使用甲种花,在正方形
部分使用甲种花,在正方形![]() 四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
(1)经了解,种植甲种花50元/![]() ,乙种花80元/
,乙种花80元/![]() ,草坪10元/
,草坪10元/![]() ,设一个矩形的面积为
,设一个矩形的面积为![]() ,装饰总费用为
,装饰总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当装饰费用为74880元时,则一个矩形区域的长和宽分别为多少?
(3)为了缩减开支,甲区域用单价为40元/![]() 的花,乙区域用单价为
的花,乙区域用单价为![]() 元/
元/![]() (
(![]() ,且
,且![]() 为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求
为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com