
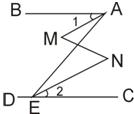
 20、如图已知,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空.)
20、如图已知,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空.) 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
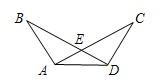 15、如图已知∠B=∠C,请同学从这①BE=CE,②AB=DC,③∠BAE=∠CDE三个等式中再选出一个作为条件,可以推出△AED是等腰三角形的有
15、如图已知∠B=∠C,请同学从这①BE=CE,②AB=DC,③∠BAE=∠CDE三个等式中再选出一个作为条件,可以推出△AED是等腰三角形的有查看答案和解析>>
科目:初中数学 来源: 题型:
 如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.
如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.查看答案和解析>>
科目:初中数学 来源:2012年人教版八年级上全等三角形2练习卷(带解析) 题型:解答题
如图,已知△ABC中,AB=AC,D、E分别是AB、AC的中点,且CD=BE,△ADC与△AEB全等吗?小明是这样分析的:因为AB=AC,BE=CD,∠BAE=∠CAD,所以△ADC≌△AEB(SSA),他的思路正确吗?请说明理由. 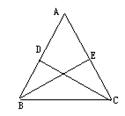
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com