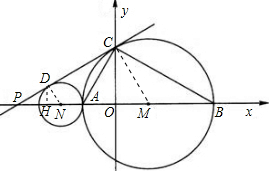
(1)证明:连接MC.
∵A(-1,0),B(3,0)
∴AO=MO,又CO⊥AM
∴AC=CM,由CM=AM
∴△ACM是正三角形;
∴AC=AM
∵PA:PB=1:2,
∴PA=AM
∴PA=AM=AC
∴∠PCM=90°
∴PC是⊙M的切线.
(2)解:∵CO
2=AO•BO,
∴C(0,

);
设过A、C、B三点的抛物线的解析式为y=a(x+1)(x-3),
则

=-3a,a=-

.
∴y=-

(x+1)(x-3).
假设满足条件的Q点存在,坐标为(m,0),并设直线QC的解析式为y=kx+b,
则
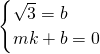
,
解得
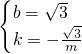
∴直线QC的解析式为y=-

x+

∵直线QC与抛物线只有一个公共点
∴方程-

(x+1)(x-3)=-

x+

有相等的实数根,
将方程整理得x
2-(2+

)x=0;
∴(2+

)
2=0,m=-

.
即满足条件的Q点存在,坐标为(-

,0).
(3)解:连接DN,作DH⊥PN,垂足为H,设⊙N的半径为r;
∵ND⊥PC,
∴ND∥MC;
∴
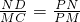
,
∴

=
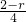
,
∴r=

.
∵DN
2=NH•NP
∴(

)
2=NH•(2-

)
∴NH=

,
∴DH=
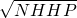
=

.
∴点D的坐标为(-2,

)
∵将抛物线y=-

(x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为y=-

(x+1)(x+3);又经验证D是该抛物线上的点.
∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点.
分析:(1)证PC是⊙M的切线,只需连接CM,证CM⊥PC即可.已知了PA:AB=1:2.因此PA=AM.根据A和B的坐标可知AB=4,因此AO=MO=1,MC=2,在直角三角形MOC中,∠CMO=60°,由此可得出三角形AMC是等边三角形,因此AC=AM=PA,由此可证得三角形PCM是直角三角形,且∠PCM=90°,由此得证.
(2)可假设符合条件的Q点存在,先设出Q点的坐标,然后根据Q和C的坐标,表示出直线QC的函数解析式,然后联立抛物线的解析式,由于这两个函数图象只有一个交点,因此联立两函数得出的一元二次方程中,△=0,可据此求出Q点的坐标.
(3)本题要先求出D点坐标,可连接DN,那么DN∥MC,即可得出关于DN,MC,PN,PM的比例关系式,即可求出圆N的半径.然后过D作DH⊥x轴于H,可在直角三角形PDN中,用射影定理求出NE的长,进而可求出DE的长,也就求出了D点的坐标.然后先求出经过平移后过P、A的抛物线的解析式,然后将D点坐标代入进行验证即可.
点评:本题以二次函数为背景,结合圆、函数图象的交点、二次函数图象的平移等问题,综合性较强.

 相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么?
相切于D.问将过A、C、B三点的抛物线平移后能否同时经过P、D、A三点,为什么? (1)证明:连接MC.
(1)证明:连接MC. );
); =-3a,a=-
=-3a,a=- .
. (x+1)(x-3).
(x+1)(x-3).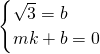 ,
,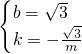
 x+
x+
 (x+1)(x-3)=-
(x+1)(x-3)=- x+
x+ 有相等的实数根,
有相等的实数根, )x=0;
)x=0; )2=0,m=-
)2=0,m=- .
. ,0).
,0).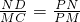 ,
, =
=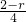 ,
, .
. )2=NH•(2-
)2=NH•(2- )
) ,
,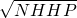 =
= .
. )
) (x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为y=-
(x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为y=- (x+1)(x+3);又经验证D是该抛物线上的点.
(x+1)(x+3);又经验证D是该抛物线上的点.

 阅读快车系列答案
阅读快车系列答案 =2,∠ADC=30°
=2,∠ADC=30°