
【题目】在平面直角坐标系中,二次函数抛物线![]() 过点
过点![]() 和
和![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求二次函数的表达式和顶点![]() 的坐标.
的坐标.
(2)将抛物线在坐标平面内平移,使其过原点,若在平移后,第二象限的抛物线上存在点![]() ,使
,使![]() 为等腰直角三角形,请求出抛物线平移后的表达式,并指出其中一种情况的平移方式.
为等腰直角三角形,请求出抛物线平移后的表达式,并指出其中一种情况的平移方式.
【答案】(1)![]() ,顶点
,顶点![]() 的坐标是
的坐标是![]() ;(2)平移后抛物线表达式是
;(2)平移后抛物线表达式是![]() ,
,![]() ,
,![]() ;原抛物线向左平移
;原抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位可得
个单位可得![]()
【解析】
(1)可以采用待定系数法求二次函数的解析式,因为点A(-1,0)、C(0,-2)在函数图象上,对称轴为x=1,也可求得A的对称点的坐标为(3,0),列方程组即可求得解析式;
(2)根据平移后的图象过原点,所以设y =﹣x+bx,使抛物线第二象限上的点P与AB组成的△ABP是等腰直角三角形,所以分三种情况来讨论,分别求出三种情况的解析式.
(1)由题意,得
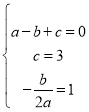 ,解得
,解得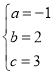
![]() 抛物线的表达式为
抛物线的表达式为![]() ;
;
当![]() 时,
时,![]() ,
,![]() 顶点
顶点![]() 的坐标是
的坐标是![]()
(2)平移后抛物线过原点,可设表达式是![]() ,分三种情况:
,分三种情况:
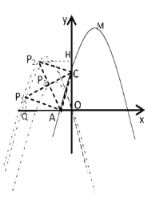
①当![]() 为等腰直角三角形
为等腰直角三角形![]() 的斜边,如图
的斜边,如图![]() 所示,做
所示,做![]() 轴于
轴于![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,所以
,所以![]() 点坐标是
点坐标是![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,![]() .
.
所以平移后抛物线表达式是![]() .
.
②当![]() 为等腰直角三角形
为等腰直角三角形![]() 的斜边,如图
的斜边,如图![]() 所示,
所示,
同上可得![]() ,
,![]() ,
,![]() ,
,
所以![]() 点坐标是
点坐标是![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,![]() .
.
所以平移后抛物线表达式是![]() .
.
③当![]() 为等腰直角三角形
为等腰直角三角形![]() 的斜边,如图
的斜边,如图![]() 所示,
所示,
这时![]() 是
是![]() 的中点,因为
的中点,因为![]() ,
,![]() ,所以
,所以![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,![]() .
.
所以平移后抛物线表达式是![]() .这时抛物线顶点是
.这时抛物线顶点是![]() ,
,
可将原抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位
个单位
综上所述,平移后抛物线表达式是![]() ,
,![]() ,
,![]() ;
;
原抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位可得
个单位可得![]()


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
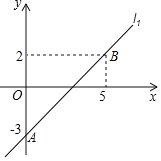
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
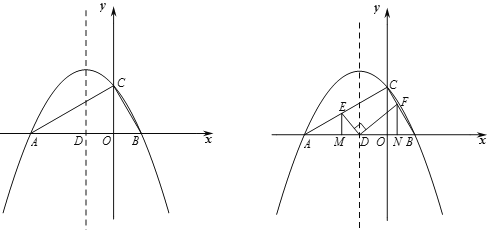
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)请直接写出![]() 、
、![]() 两点的坐标及
两点的坐标及![]() 的度数;
的度数;
(2)如图1,若点![]() 为抛物线对称轴上的点,且
为抛物线对称轴上的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图![]() ,若点
,若点![]() 、
、![]() 分别为线段
分别为线段![]() 和
和![]() 上的动点,且
上的动点,且![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .在
.在![]() 、
、![]() 两点的运动过程中,试探究:
两点的运动过程中,试探究:
①![]() 是否是一个定值?如果是,请求出这个定值,如果不是,请说明理由;
是否是一个定值?如果是,请求出这个定值,如果不是,请说明理由;
②若将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,当点
,当点![]() 从点
从点![]() 运动到点
运动到点![]() 的过程中,求点
的过程中,求点![]() 和点
和点![]() 的运动轨迹的长度之和.
的运动轨迹的长度之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为评估九年级学生在“新冠肺炎”疫情期间“空中课堂”的学习效果,某中学抽取了部分参加调研测试的学生成绩作为样本,并把样本分为优、良、中、差四类,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
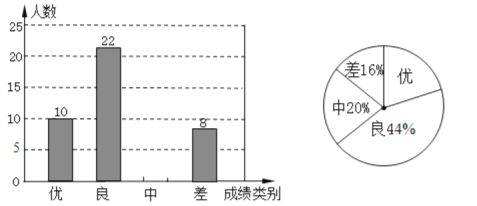
(1)在这次调查中,一共抽取了多少名学生;
(2)通过计算补全条形统计图;
(3)该校九年级共有320人参加了这次调研测试,请估算该校九年级共有多少名学生的成绩达到了优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开展阳光体育运动,掌握运动技能,增强身体素质.某校初二年级五月开展了周末一小时兴趣锻炼活动,项目包括:篮球技能、排球技能、足球技能、立定跳远、50米跑,每个同学只选一项参与.王老师为了解学生对各种项目的参与情况,随机调查了部分学生参与哪一类项目(被调查的学生没有不参与的),并将调查结果制成了如下的两个统计图(不完整)请你根据图中所提供的信息,完成下列问题:
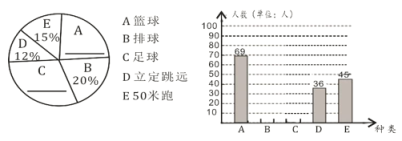
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出足球项目在扇形统计图中所占圆心角的度数;
(3)若该中学初二年级有![]() 名学生,请估计该校初二学生参与球类项目的人数.
名学生,请估计该校初二学生参与球类项目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com