
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是____.

【答案】π﹣2.
【解析】
连接CD,作DM⊥BC,DN⊥AC,证明△DMG≌△DNH,则S四边形DGCH=S四边形DMCN,求得扇形FDE的面积,则阴影部分的面积即可求得.
连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,∴DC=![]() AB=2,四边形DMCN是正方形,DM=
AB=2,四边形DMCN是正方形,DM=![]() .
.
则扇形FDE的面积是:![]() =π.
=π.
∵CA=CB,∠ACB=90°,点D为AB的中点,∴CD平分∠BCA.
又∵DM⊥BC,DN⊥AC,∴DM=DN.
∵∠GDH=∠MDN=90°,∴∠GDM=∠HDN.在△DMG和△DNH中,∵ ,∴△DMG≌△DNH(AAS),∴S四边形DGCH=S四边形DMCN=2.
,∴△DMG≌△DNH(AAS),∴S四边形DGCH=S四边形DMCN=2.
则阴影部分的面积是:π﹣2.
故答案为:π﹣2.


科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2![]() .正确结论的个数有( )
.正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
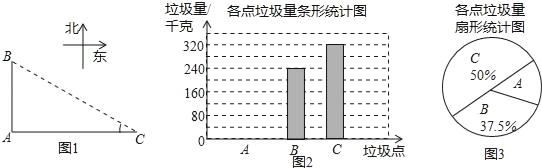
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=![]() (x>0)的图象经过点D.
(x>0)的图象经过点D.
(1)求点D的坐标及反比例函数的解析式;
(2)经过点C的一次函数y=kx+b(k≠0)的图象与反比例函数的图象交于P点,当k>0时,确定点P横坐标的取值范围(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图①,一条笔直的公路上有A、B、C三地,B.C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图像进行以下探究:

(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图像,求甲车到A地的距离y1与行驶时间x的函数表达式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车(两种车型都要有)每年能节省的汽油量不低于22.4万升,请问有哪几种购车方案?
(3)求(2)中最省钱的购买方案所需的购车款.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(-3,3),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.过点A作AD⊥x轴,垂足为D,当DC=1时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,则点M的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴的交点坐标分别为A(1,0),B(x2,0)(点B在点A的右侧),其对称轴是x=3,该函数有最小值是﹣2.
(1)求二次函数解析式;
(2)在图1上作平行于x轴的直线,交抛物线于C(x3,y3),D(x4,y4),求x3+x4的值;
(3)将(1)中函数的部分图象(x>x2)向下翻折与原图象未翻折的部分组成图象“G”,如图2,在(2)中平行于x轴的直线取点E(x5,y5)、(x4<x5),结合函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com