
阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt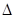 ABC
中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC
中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt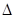 ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
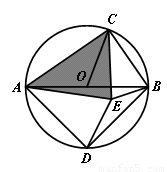
1求证: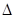 ACE是奇异三角形;
ACE是奇异三角形;
2当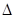 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
解:(1)真命题
(2)在Rt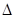 ABC
中a2+b2= c2,
ABC
中a2+b2= c2,
∵c>b>a>0
∴2c2>a2+b2,2a2<c2+b2
∴若Rt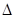 ABC是奇异三角形,一定有2b2=c2+ a2
ABC是奇异三角形,一定有2b2=c2+ a2
∴2b2=a2+(a2+b2)
∴b2=2a2 得:b= a
a
∵c2=b2+ a2=3a2
∴c=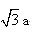
∴a:b: c=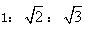
(3)1∵AB是⊙O的直径ACBADB=90°
在Rt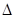 ABC 中,AC2+BC2=AB2
ABC 中,AC2+BC2=AB2
在Rt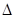 ADB 中,AD2+BD2=AB2
ADB 中,AD2+BD2=AB2
∵点D是半圆的中点
∴=
∴AD=BD
∴AB2=AD2+BD2=2AD2
∴AC2+CB2=2AD2
又∵CB=CE,AE=AD
∴AC2=CE2=2AE2
∴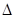 ACE是奇异三角形
ACE是奇异三角形
2由1可得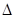 ACE是奇异三角形
ACE是奇异三角形
∴AC2=CE2=2AE2
当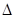 ACE是直角三角形时
ACE是直角三角形时

【解析】(1)根据“奇异三角形”的定义与等边三角形的性质,求证即可;
(2)根据勾股定理与奇异三角形的性质,可得a2+b2=c2与a2+c2=2b2,用a表示出b与c,即可求得答案;
(3)①AB是⊙O的直径,即可求得∠ACB=∠ADB=90°,然后利用勾股定理与圆的性质即可证得;
②利用(2)中的结论,分别从AC:AE:CE=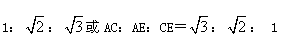 去分析,即可求得结果.
去分析,即可求得结果.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2012-2013学年浙江温州育英学校八年级10月月考数学试卷1(带解析) 题型:解答题
阅读下面的情境对话,然后解答问题
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt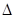 ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt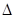 ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
1求证: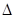 ACE是奇异三角形;
ACE是奇异三角形;
2当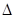 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com