
 如图,菱形ABCD中,BP=CP,MN∥AB,求证:
如图,菱形ABCD中,BP=CP,MN∥AB,求证:分析 (1)先根据菱形的定义得:AB∥CD,再根据MN∥AB得:MN∥AB∥CD,可知△ANM∽△ADC,△ABN∽△QDN,然后根据相似三角形的性质即可得证;
(2)根据平行证明△ABP∽△MNP,列比例式后,再证明PA=PN即可得出;
(3)先根据菱形的性质:菱形的一条对角线平分一组对角得:∠BAC=∠PAN,从而证明△ABP∽△NBA,列比例式可得结论;
(4)根据角平分线的性质得比例式即可.
解答 解:(1)∵四边形ABCD是菱形,
∴AB∥CD,
∵MN∥AB,
∴MN∥AB∥CD,
∴△ANM∽△ADC,△ABN∽△DQN,
∴$\frac{AM}{MC}=\frac{AN}{ND}$,$\frac{AN}{ND}=\frac{AB}{QD}$,
∴$\frac{AM}{MC}$=$\frac{AB}{QD}$,
(2)∵MN∥AB,
∴△ABP∽△MNP,
∴$\frac{PA}{PM}=\frac{PB}{PN}$,
∵PB=PC,
∴∠PBC=∠PCB,
∵AD∥BC,
∴∠PBC=∠PNA,∠PCB=∠PAN,
∴∠PNA=∠PAN,
∴PA=PN,
∴$\frac{PA}{PM}=\frac{PC}{PA}$,
∴PA2=PM•PC;
(3)∵四边形ABCD是菱形,
∴∠BAC=∠PAN,
∵∠PAN=∠PNA,
∴∠BAC=∠PNA,
∵∠ABP=∠ABP,
∴△ABP∽△NBA,
∴$\frac{AB}{BP}=\frac{BN}{AB}$,
∴AB2=BP•BN;
(4)∵∠BAC=∠PAN,
∴$\frac{AB}{AN}$=$\frac{PB}{PN}$.
点评 本题考查了菱形的性质、相似三角形的性质和判定、角平分线的性质;能利用平行证明相应的三角形相似是关键,并熟练掌握利用乘积式化为比例式确定证明哪两个三角形.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
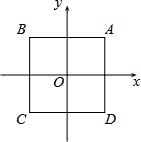 如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
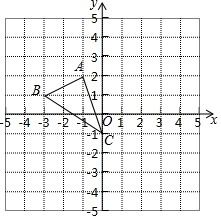 如图,在平面直角坐标系xOy中,已知A(-1,2),B(-3,1)C(0,-1)
如图,在平面直角坐标系xOy中,已知A(-1,2),B(-3,1)C(0,-1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com