
【题目】已知:如图,点![]() 在双曲线
在双曲线![]() (其中
(其中![]() )上,点
)上,点![]() 在双曲线
在双曲线![]() (其中
(其中![]() )上,点
)上,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 、
、![]() 、
、![]() 、
、![]() 围成的四边形为正方形.
围成的四边形为正方形.
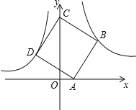
![]() 求
求![]() 的值;
的值;
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
【答案】(1)k=9;(2)a=1.
【解析】
(1)把B的坐标代入求出即可;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,证△DAE≌△ABF,推出DE=AF=3﹣a,AE=FB=3,OE=3﹣a,从而求得D的坐标(a﹣3,3﹣a),代入y=![]() 即可求得a的值.
即可求得a的值.
(1)∵点B(3,3)在双曲线y=![]() (其中x>0)上,∴3=
(其中x>0)上,∴3=![]() ,∴k=3×3=9;
,∴k=3×3=9;
(2)过D作DE⊥x于点E,过点B作BF⊥x于点F,则∠DEA=∠AF B=90°.
∵点B(3,3),∴BF=3,OF=3.
∵A的坐标为(a,0),∴OA=a,AF=3﹣a.
∵四边形ABCD是正方形,∴AD=AB,∠DAB=90°,∴∠DAE+∠BAF=90°.
又∵∠DAE+∠ADE=90°,∴∠ADE=∠BAF.
在△DAE和△ABF中,∵ ,∴△DAE≌△ABF(AAS),∴DE=AF=3﹣a,AE=FB=3,∴OE=3﹣a.
,∴△DAE≌△ABF(AAS),∴DE=AF=3﹣a,AE=FB=3,∴OE=3﹣a.
又∵点D在第二象限,∴D(a﹣3,3﹣a).
∵点D在双曲线y=![]() (其中x<0)上,∴3﹣a=
(其中x<0)上,∴3﹣a=![]() ,∴a=1或a=5(不合题意,舍去),∴a=1.
,∴a=1或a=5(不合题意,舍去),∴a=1.


科目:初中数学 来源: 题型:
【题目】如图所示,把多块大小不同的![]() 角三角板,摆放在平面直角坐标系中,第一块三角板
角三角板,摆放在平面直角坐标系中,第一块三角板![]() 的一条直角边与
的一条直角边与![]() 轴重合且点
轴重合且点![]() 的坐标为
的坐标为![]() ,
,![]() ,第二块三角板的斜边
,第二块三角板的斜边![]() 与第一块三角板的斜边
与第一块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,第三块三角板的斜边
,第三块三角板的斜边![]() 与第二块三角板的斜边
与第二块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,第四块三角板斜边
,第四块三角板斜边![]() 与第三块三角板的斜边
与第三块三角板的斜边![]() 垂直且交
垂直且交![]() 轴于点
轴于点![]() ,按此规律继续下去,则点
,按此规律继续下去,则点![]() 的坐标为( )
的坐标为( )
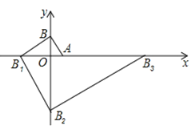
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石景山某中学初三![]() 班环保小组的同学,调查了本班
班环保小组的同学,调查了本班![]() 名学生自己家中一周内丢弃的塑料袋的数量,数据如下(单位:个)
名学生自己家中一周内丢弃的塑料袋的数量,数据如下(单位:个)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若一个塑料袋平铺后面积约为
.若一个塑料袋平铺后面积约为![]() ,利用上述数据估计如果将全班
,利用上述数据估计如果将全班![]() 名同学的家庭在一周内共丢弃的塑料袋全部铺开,面积约为( )
名同学的家庭在一周内共丢弃的塑料袋全部铺开,面积约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() OAB与
OAB与![]() ODC是位似图形 。
ODC是位似图形 。
试问:(1)AB与CD平行吗?请说明理由 。
(2)如果OB=3,OC=4,OD=3.5.试求![]() OAB与
OAB与![]() ODC的相似比及OA的长 。
ODC的相似比及OA的长 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用![]() 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为![]() .
.
![]() 求这矩形仓库的长;
求这矩形仓库的长;
![]() 有规格为
有规格为![]() 和
和![]() (单位:
(单位:![]() )的地板砖单价分别为
)的地板砖单价分别为![]() 元/块和
元/块和![]() 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
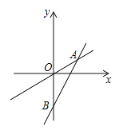
(1)求一次函数的表达式;
(2)求两直线与![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,若存在,直接写出
为腰的等腰三角形,若存在,直接写出![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com