
如图,点C在BD上,在线段BD的同侧作等边△ABC和等边△CDE,AD、BE相交于点F.
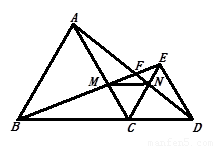
(1)求证:BE=AD;
(2)求∠AFB的度数;
(3)设BE与AC交于点M,CE与AD交于点N,连接MN,试判断△MCN的形状,并说明理由.
(1)证明见解析;(2)∠AFB=60°;(3)△MCN是等边三角形, 证明见解析.
【解析】
试题分析:(1)证明线段相等的常用方法是三角形的全等,而包括线段BE和线段AD的三角形为△BCE和△ACD,下面就找全等的条件,因为△ABC和△CDE是等边三角形,所以BC=AC,CE=CD, ∠ACB=∠DCE= 60°,所以∠ACE=60°, ∠BCE=∠ACD= 120°,所以在△BCE和△ACD中,BC=AC, ∠BCE=∠ACD CE=
CD,所以△BCE≌△ACD,所以BE=AD; (2)三角形的一个外角等于与它不相邻的两个内角和,由题, ∠AFB是△BFD的一个外角,所以∠AFB=∠CBE+∠ADC,有(1)知△BCE≌△ACD,所以∠CBE=∠CAD,所以∠AFB
=∠CBE+∠ADC=∠CAD+∠ADC=∠ACB=60°(∠ACB是△ACD的一个外角);(3)直观上看△MCN是等边三角形,由(1)知∠MCN=60°,只要证明MC=NC,包含这两条线段的三角形有△BCM和△ACN,由(2)知, ∠CBE=∠CAD,BC=AC, ∠ACB=∠ACN= 60°,所以△BCM≌△CAN,所以MC=NC.
试题解析:(1)∵△ABC和△CDE是等边三角形,
∴BC=AC,CE=CD, ∠ACB=∠DCE= 60°,
∴∠ACE=60°, ∠BCE=∠ACD= 120°,
在△BCE和△ACD中,BC=AC, ∠BCE=∠ACD CE=CD,
∴△BCE≌△ACD,
∴BE=AD;
(2)∠AFB是△BFD的一个外角,
∴∠AFB=∠CBE+∠ADC,
有(1)知△BCE≌△ACD,
∴∠CBE=∠CAD,
∴∠AFB=∠CBE+∠ADC=∠CAD+∠ADC=∠ACB=60°(∠ACB是△ACD的一个外角);
(3)由(2)知, 在△BCM和△CAN中,∠CBE=∠CAD,BC=AC, ∠ACB=∠ACN= 60°,
∴△BCM≌△CAN,
∴MC=NC,
由(1)知∠MCN=60°,
∴△MCN是等边三角形
考点:等边三角形和三角形的全等.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
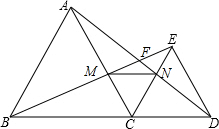 如图,点C在BD上,在线段BD的同侧作等边△ABC和等边△CDE,AD、BE相交于点F.
如图,点C在BD上,在线段BD的同侧作等边△ABC和等边△CDE,AD、BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com