
如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
解:(1)如图1,作AH⊥BC于H,则∠AHB=90°。
∵△ABC是等边三角形,∴AB=BC=AC=3。
∵∠AHB=90°,∴BH= BC=
BC= 。
。
在Rt△ABH中,由勾股定理,得AH= 。
。
∴ 。
。
(2)如图2,当0<x≤ 时,
时, 。
。
作AG⊥DE于G,∴∠AGD=90°,∠DAG=30°。
∴DG=x,AG= 。
。
∴ 。
。
如图3,当 <x<3时,作MG⊥DE于G,
<x<3时,作MG⊥DE于G,
∵AD=x,∴BD=DM=3-x,
∴DG= ,MF=MN=2x-3,MG=
,MF=MN=2x-3,MG=
∴ 。
。
综上所述,y关于x的函数解析式为 。
。
(3)当0<x≤ 时,
时,
∵a= >0,开口向上,在对称轴的右侧y随x的增大而增大,
>0,开口向上,在对称轴的右侧y随x的增大而增大,
∴x= 时,
时, 。
。
当 <x<3时,
<x<3时, ,
,
∵a= <0,开口向下,∴x=2时,
<0,开口向下,∴x=2时,
∵ >
> ,∴y最大时,x=2。
,∴y最大时,x=2。
∴DE=2,BD=DM=1。
如图4,作FO⊥DE于O,连接MO,ME,
∴DO=OE=1。∴DM=DO。
∵∠MDO=60°,∴△MDO是等边三角形。
∴∠DMO=∠DOM=60°,MO=DO=1。
∴MO=OE,∠MOE=120°。
∴∠OME=30°。∴∠DME=90°。
∴DE是直径。
∴ 。
。
解析


科目:初中数学 来源: 题型:解答题
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,若这种商品每件的销售价每提高0.5元,其销售量就减少10件.问(1)每件售价定为多少元时,才能使利润为640元?(2)每件售价定为多少元时,才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线C1的顶点为P(1,0),且过点(0, ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
(1)求抛物线C1的解析式的一般形式;
(2)当m=2时,求h的值;
(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF﹣tan∠ECP=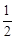 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,已知抛物线 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线 与直线y=x交于点A,点B在直线
与直线y=x交于点A,点B在直线 上,∠BOA=90°.抛物线
上,∠BOA=90°.抛物线 过点A,O,B,顶点为点E.
过点A,O,B,顶点为点E.
(1)求点A,B的坐标;
(2)求抛物线的函数表达式及顶点E的坐标;
(3)设直线y=x与抛物线的对称轴交于点C,直线BC交抛物线于点D,过点E作FE∥x轴,交直线AB于点F,连接OD,CF,CF交x轴于点M.试判断OD与CF是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
(1)点C的坐标是 ,线段AD的长等于 ;
(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点G,M,求抛物线的解析式;
(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com