
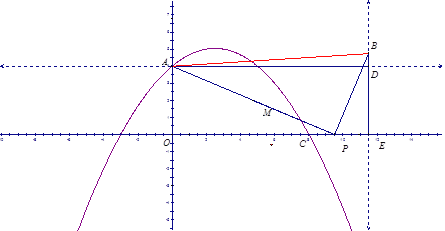
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+![]() x+cЙ§ЕуAЃЈ0ЃЌ4ЃЉКЭCЃЈ8ЃЌ0ЃЉЃЌPЃЈtЃЌ0ЃЉЪЧxжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌMЪЧЯпЖЮAPЕФжаЕуЃЌНЋЯпЖЮMPШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЯпЖЮPBЃЎЙ§ЕуBзїxжсЕФДЙЯпЁЂЙ§ЕуAзїyжсЕФДЙЯпЃЌСНжБЯпЯрНЛгкЕуDЃЎ
x+cЙ§ЕуAЃЈ0ЃЌ4ЃЉКЭCЃЈ8ЃЌ0ЃЉЃЌPЃЈtЃЌ0ЃЉЪЧxжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌMЪЧЯпЖЮAPЕФжаЕуЃЌНЋЯпЖЮMPШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЯпЖЮPBЃЎЙ§ЕуBзїxжсЕФДЙЯпЁЂЙ§ЕуAзїyжсЕФДЙЯпЃЌСНжБЯпЯрНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФЖдГЦжсЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЕуDТфдкХзЮяЯпЩЯЃП
ЃЈ3ЃЉЪЧЗёДцдкtЃЌЪЙЕУвдAЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїPEBЯрЫЦЃПШєДцдкЃЌЧѓДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉЖдГЦжсЮЊЃКx=![]() ЃЛЃЈ2ЃЉЕБt=3ЪБЃЌЕуDТфдкХзЮяЯпЩЯЃЛЃЈ3ЃЉЕБt=Љ2+2
ЃЛЃЈ2ЃЉЕБt=3ЪБЃЌЕуDТфдкХзЮяЯпЩЯЃЛЃЈ3ЃЉЕБt=Љ2+2![]() ЁЂt=8+4
ЁЂt=8+4![]() ЪБЃЌвдAЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїPEBЯрЫЦЃЎ
ЪБЃЌвдAЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїPEBЯрЫЦЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЬтвтРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЌДгЖјЕУЕНЖдГЦжсЃЛЃЈ2ЃЉИљОнЬтвтЕУГіЕуMЕФзјБъЃЌИљОна§зЊЕФаджЪЕУГіЕуEКЭЕуBЕФзјБъЃЌДгЖјЕУЕНЕуDЕФзјБъЃЌШЛКѓЧѓГіtЕФжЕЃЛЃЈ3ЃЉЗж0ЃМtЃМ8КЭtЃО8СНжжЧщПіЃЌУПжжЧщПіЗжСНжжЧщПіНјааЬжТлМЦЫуЃЌЕУГіtЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтЕУЃЌ ЃЌНтЕУ
ЃЌНтЕУ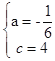 ЃЎ
ЃЎ
![]() ХзЮяЯпЕФНтЮіЪНЮЊЃК
ХзЮяЯпЕФНтЮіЪНЮЊЃК ![]() ЃЌЫќЕФЖдГЦжсЮЊЃК
ЃЌЫќЕФЖдГЦжсЮЊЃК ![]()
ЃЈ2ЃЉгЩЬтвтЕУЃК ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
![]() ЪЧ
ЪЧ![]() ШЦЕуPЫГЪБеыа§зЊ90ЁуЖјЕУЃЌ
ШЦЕуPЫГЪБеыа§зЊ90ЁуЖјЕУЃЌ ![]()
![]() ЃЌ
ЃЌ ![]() ЃЎДгЖјга
ЃЎДгЖјга![]() ЃЎ
ЃЎ
МйЩш![]() дкХзЮяЯпЩЯЃЌга
дкХзЮяЯпЩЯЃЌга![]() ЃЌ НтЕУ
ЃЌ НтЕУ![]()
Ёп![]() ЃЌМДЕБ
ЃЌМДЕБ![]() ЪБЃЌЕуDТфдкХзЮяЯпЩЯЃЎ
ЪБЃЌЕуDТфдкХзЮяЯпЩЯЃЎ
ЃЈ3ЃЉЂйЕБ![]() ЪБЃЌШчЭМЃЌ
ЪБЃЌШчЭМЃЌ
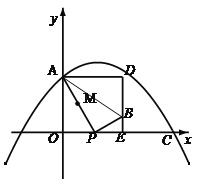
![]() ЃЌ
ЃЌ
ЃЈ1ЃЉШєЁї![]() ЁзЁїADBЃЌДЫЪБ
ЁзЁїADBЃЌДЫЪБ![]() ЃЌгаЃК
ЃЌгаЃК ![]() ЃЌ ЃЌМД
ЃЌ ЃЌМД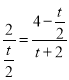 ЃЌ
ЃЌ
ЛЏМђЕУ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЮоНтЁЃ
ЮоНтЁЃ
ШєЁї![]() ЁзЁїADBЃЌ ДЫЪБ
ЁзЁїADBЃЌ ДЫЪБ![]() ЃЌгаЃК
ЃЌгаЃК ![]() ЃЌ ЃЌМД
ЃЌ ЃЌМД ЃЌ
ЃЌ
ЛЏМђЕУЃК ![]() ЃЌЙигк
ЃЌЙигк![]() ЕФвЛдЊЖўДЮЗНГЬЕФХаБ№ЪН
ЕФвЛдЊЖўДЮЗНГЬЕФХаБ№ЪН![]() ЃЌ
ЃЌ
гЩЧѓИљЙЋЪНЕУЃК![]()
![]() ЃЌ
ЃЌ ![]() ЁЃ
ЁЃ
ЂкЕБ![]() ЪБЃЌШчЭМЂкЃЌШєЁїPOAЁзЁїADB
ЪБЃЌШчЭМЂкЃЌШєЁїPOAЁзЁїADB![]()
ЃЈ1ЃЉШєЁї![]() ЁзЁїADBЃЌДЫЪБ
ЁзЁїADBЃЌДЫЪБ![]() ЃЌгаЃК
ЃЌгаЃК
![]() ЃЌМД
ЃЌМД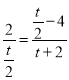 ЃЌЛЏМђЕУ
ЃЌЛЏМђЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈИКИљЩсШЅЃЉЁЃ
ЃЈИКИљЩсШЅЃЉЁЃ
ЃЈ2ЃЉШєЁї![]() ЁзЁїADBЃЌЭЌРэЕУДЫЪБ
ЁзЁїADBЃЌЭЌРэЕУДЫЪБ![]() ЮоНтЁЃ
ЮоНтЁЃ
злКЯЩЯЪіЃКЕБ![]() ЁЂ
ЁЂ![]() ЪБЃЌвдAЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїPEBЯрЫЦЁЃ
ЪБЃЌвдAЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїPEBЯрЫЦЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНЬѕжБЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌШєЁЯ1КЭЁЯ2ЪЧЭЌХдФкНЧЃЌЧвЁЯ1=75ЁуЃЌдђЁЯ2ЮЊЃЈ ЃЉ
A.75Ёу
B.105Ёу
C.75ЁуЛђ105Ёу
D.ДѓаЁВЛШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўдЊвЛДЮЗНГЬ2xЉyЃН3ЃЌгУКЌxЕФЪНзгБэЪОyЕФаЮЪНЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзд2009ФъЦ№ЃЌУПФъЕФ11дТ11ШеЪЧTmallвЛФъвЛЖШШЋГЁДѓДйЯњЕФШезг.ФГЗўЪЮЕъЖдФГЩЬЦЗЭЦГіДйЯњЛюЖЏ:ЫЋЪЎвЛЕБЬьЃЌТђСНМўЕШжЕЕФЩЬЦЗПЩдкУПМўдМлМѕ50дЊЕФЛљДЁЩЯЃЌдйДђАЫелЃЛШчЙћЕЅТђЃЌдђАДдМлЙКТђ.
ЃЈ1ЃЉФнФнПДжаСНМўдМлЖМЪЧ300дЊЕФДЫРрЩЬЦЗЃЌ дђдкЫЋЪЎвЛЕБЬьЃЌЙКТђетСНМўЩЬЦЗзмЙВашвЊЖрЩйЧЎ?
ЃЈ2ЃЉамамЙКТђСЫСНМўЕШжЕЕФДЫРрЩЬЦЗКѓЃЌ ЗЂЯжБШСНМўвЛЦ№АДдМлСљелЙКТђБувЫ. ШєетСНМўЕШжЕЩЬЦЗЕФМлИёЖМЪЧДѓгк196ЕФећЪ§ЃЌ дђдМлПЩФмЪЧЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцзјБъзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЖЈвхШчЯТЃКЕБ
ЕФзјБъЖЈвхШчЯТЃКЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
вбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЕу
ЃЉЕу![]() ЕФБфЛЛЕу
ЕФБфЛЛЕу![]() ЕФзјБъЪЧ__________ЃЎ
ЕФзјБъЪЧ__________ЃЎ
Еу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() __________ЃЎ
__________ЃЎ
ЃЈ![]() ЃЉЕу
ЃЉЕу![]() ЕФБфЛЛЕуЮЊ
ЕФБфЛЛЕуЮЊ![]() ЃЌЫцзХ
ЃЌЫцзХ![]() ЕФБфЛЏЃЌЕу
ЕФБфЛЏЃЌЕу![]() ЛсдЫЖЏЦ№РДЃЌЧыдкБИгУЭМЃЈ
ЛсдЫЖЏЦ№РДЃЌЧыдкБИгУЭМЃЈ![]() ЃЉжаЛГіЕу
ЃЉжаЛГіЕу![]() ЕФдЫЖЏТЗОЖЃЎ
ЕФдЫЖЏТЗОЖЃЎ
ЃЈ![]() ЃЉШє
ЃЉШє![]() ЪЧЕШбќШ§НЧаЮЃЌЧыжБНгаДГіДЫЪБ
ЪЧЕШбќШ§НЧаЮЃЌЧыжБНгаДГіДЫЪБ![]() ЕФжЕЃК__________ЃЎ
ЕФжЕЃК__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌШєЕуAЃЈЉ2ЃЌnЃЉЃЌBЃЈ1ЃЌЉ2ЃЉЪЧвЛДЮКЏЪ§y=kx+bЕФЭМЯѓКЭЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжБЯпABгыxжсЕФНЛЕуCЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЕуOЕНжБЯпABЕФОрРыЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃy3n+1ЁТyn+1ЃН__________ЃЌ[(Ѓm)3]2ЃН___________;
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЪ§420000гУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈЁЁЁЁЃЉ
A. 420ЁС103B. 42ЁС104C. 4.2ЁС105D. 0.42ЁС106
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§БШР§КЏЪ§y=(2m+4)xЃЌЧѓЃК
(1)mЮЊКЮжЕЪБЃЌКЏЪ§ЭМЯѓОЙ§ЕквЛЁЂШ§ЯѓЯоЃП
(2)mЮЊКЮжЕЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃП
(3)mЮЊКЮжЕЪБЃЌЕу(1ЃЌ3)дкИУКЏЪ§ЕФЭМЯѓЩЯЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com