
如图,在△ 和△
和△ 中,
中, ,
, 为线段
为线段 上一点,且
上一点,且 .
.
求证: .
.
科目:初中数学 来源: 题型:解答题
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分. 问:点C在什么位置时,分割得到的三角形与Rt△OAB相似?(注:在图上画出所有符合要求的线段PC,并写出相应的点C的坐标).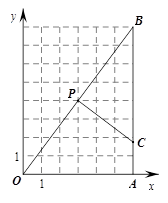
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆为3.1米,且BC=1米,CD=5米,请你根据所给出的数据求树高ED.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图①,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)( ),解答下列问题:
),解答下列问题:
(1)当 为何值时,PQ∥BC?
为何值时,PQ∥BC?
(2)设△AQP的面积为y( ),求y与t之间的函数关系式;
),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻 ,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,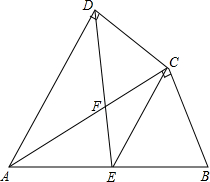
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求  的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com