
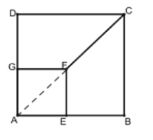
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
【答案】(1)①![]() ,②45°;(2)仍然成立,见解析;(3)
,②45°;(2)仍然成立,见解析;(3)![]()
【解析】
(1)根据正方形的性质即可得出答案;
(2)过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,即可得出答案;
是平行四边形,即可得出答案;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,再过点D作DM⊥GH于点M,证出GM=
是平行四边形,再过点D作DM⊥GH于点M,证出GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG,再利用勾股定理计算即可得出答案.
DG,再利用勾股定理计算即可得出答案.
解:(1)①线段![]() 与
与![]() 的数量关系为
的数量关系为![]() ;
;
②直线![]() 与
与![]() 所夹锐角的度数为45°.
所夹锐角的度数为45°.
连接AF,根据正方形的性质可得A、F、C三点共线,∠CAD=45°
∵AF=![]() AG,AC=
AG,AC=![]() AD
AD
∴CF=AC-AF=![]() (AD-AG)=
(AD-AG)=![]() DG
DG
(2)仍然成立,证明如下:
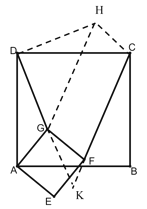
过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,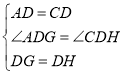
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]() ,∴
,∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
在![]() 中,
中,![]()
∴![]() ,
,
即![]() ,
,
∵![]()
∴![]() ,即直线
,即直线![]() 与
与![]() 所夹锐角的度数为45°;
所夹锐角的度数为45°;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]()
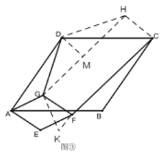
∵四边形![]() 是菱形 ,
是菱形 ,![]()
∴![]() ,∠ADC=120°
,∠ADC=120°
∵∠GDH=120°
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,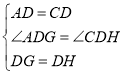
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是菱形
是菱形
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
过点D作DM⊥GH于点M
∴GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG
DG
在Rt△DGM中,![]()
∴GM=![]() DG,
DG,
∴DG:CF=![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
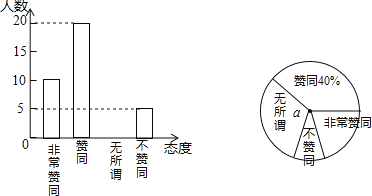
(1)在这次问卷调查中,一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 °;
(4)若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把二元一次方程![]() 的一个解用一个点表示出来,例如:可以把它的其中一个解
的一个解用一个点表示出来,例如:可以把它的其中一个解![]() 用点(2,1 )在平面直角坐标系中表示出来
用点(2,1 )在平面直角坐标系中表示出来
探究1:
(1)请你在直角坐标系中标出4个以方程![]() 的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
在这条直线上任取一点,这个点的坐标是方程![]() 的解吗? (填“是”或“不是”___
的解吗? (填“是”或“不是”___
(2)以方程![]() 的解为坐标的点的全体叫做方程
的解为坐标的点的全体叫做方程![]() 的图象.根据上面的探究想一想:方程
的图象.根据上面的探究想一想:方程![]() 的图象是_ _.
的图象是_ _.

探究2:根据上述探究结论,在同-平面直角坐标系中画出二元一次方程组![]() 中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组
中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组![]() 的解,即
的解,即
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
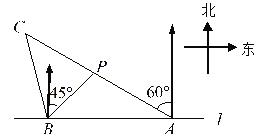
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E、F是BC上一点,且CF=AE,连接DF.
(1)求证:四边形BEDF是平行四边形;
(2)若∠ABC=70°,求∠CDF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com