
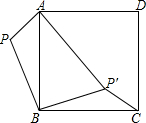
 如图所示,已知P为正方形ABCD外的一点.PA=1,PB=2.将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,求∠BP′C的度数.
如图所示,已知P为正方形ABCD外的一点.PA=1,PB=2.将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,求∠BP′C的度数.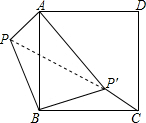 解:连接PP′,
解:连接PP′,| PB2+P′B2 |
| 2 |


科目:初中数学 来源: 题型:
 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•黄石)如图所示,已知A(
(2012•黄石)如图所示,已知A(| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源:2013届浙江省桐乡三中九年级上学期期中考试数学试卷(带解析) 题型:单选题
如图所示,已知 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点 在
在 正半轴上运动,当线段
正半轴上运动,当线段 与线段
与线段 之差达到最大时,点
之差达到最大时,点 的坐标是( )
的坐标是( )
A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省九年级上学期期中考试数学试卷(解析版) 题型:选择题
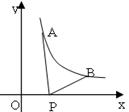
如图所示,已知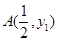 ,
,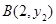 为反比例函数
为反比例函数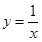 图像上的两点,动点
图像上的两点,动点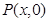 在
在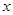 正半轴上运动,当线段
正半轴上运动,当线段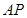 与线段
与线段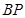 之差达到最大时,点
之差达到最大时,点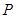 的坐标是( )
的坐标是( )
A. 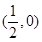 B.
B.
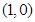 C.
C.
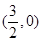 D.
D.
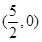
查看答案和解析>>
科目:初中数学 来源:湖北省中考真题 题型:单选题
 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点 在
在 正半轴上运动,当线段
正半轴上运动,当线段 与线段
与线段 之差达到最大时,点
之差达到最大时,点 的坐标是
的坐标是




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com