【题目】如图，在
中，
.
⑴已知线段AB的垂直平分线与BC边交于点P，连结AP，求证：
；
⑵以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连结AQ，若
，求
的度数.
【答案】（1）见解析；（2）∠B=36°.
【解析】
（1）根据垂直平分线的性质，得到PA=PB，再由等腰三角形的性质得到∠PAB=∠B，从而得到答案；
（2）根据等腰三角形的性质得到∠BAQ=∠BQA，设∠B=x，由题意得到等式∠AQC=∠B+∠BAQ=3x，即可得到答案.
（1）证明：因为点P在AB的垂直平分线上，
所以PA=PB，
所以∠PAB=∠B，
所以∠APC=∠PAB+∠B=2∠B.
（2）根据题意，得BQ=BA，
所以∠BAQ=∠BQA，
设∠B=x，
所以∠AQC=∠B+∠BAQ=3x，
所以∠BAQ=∠BQA=2x，
在△ABQ中，x+2x+2x=180°，
解得x=36°，即∠B=36°.
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直于x轴，垂足为点B，反比例函数y=
（x＜0）的图象经过AO的中点C，交AB于点D．若点D的坐标为（﹣4，n），且AD=3．
（1）求反比例函数y=的表达式；
（2）求经过C、D两点的直线所对应的函数解析式；
（3）设点E是线段CD上的动点（不与点C、D重合），过点E且平行y轴的直线l与反比例函数的图象交于点F，求△OEF面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC和△ADE均为等腰直角三角形，连接BE，点F、G分别为AD、AC的中点，连接FG．在△ADE绕A旋转的过程中，当B、D、E三点共线时，AB=
，AD=1，则线段FG的长为___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们已经知道，形如
的无理数的化简要借助平方差公式：
例如：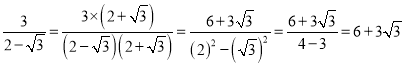
。
下面我们来看看完全平方公式在无理数化简中的作用。
问题提出：
该如何化简？
建立模型：形如
的化简，只要我们找到两个数
，使
，这样
，
，那么便有：
，
问题解决：化简，
解：首先把化为
，这里
，
，由于4+3=7，
，
即（
，
，
∴
模型应用1：
利用上述解决问题的方法化简下列各式：
（1）
；（2）
；
模型应用2：
（3）在
中，
，
，
，那么
边的长为多少？（结果化成最简）。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，
是
内的一点.
（1）如图，
平分
交
于点
，点在线段上（点不与点
、重合），且
，求证：
.
（2）如图，若是等边三角形，
，
，以
为边作等边
，连
.当
是等腰三角形时，试求出
的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=AC，∠A=30°，AB=16，以AB为直径的⊙O与BC边相交于点D，与AC交于点F，过点D作DE⊥AC于点E．
（1）求证：DE是⊙O的切线；
（2）求CE的长；
（3）过点B作BG∥DF，交⊙O于点G，求弧BG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】反比例函数y=
的图象向右平移
个单位长度得到一个新的函数，当自变量x取1，2，3，4，5，…，（正整数）时，新的函数值分别为y1，y2，y3，y4，y5，…，其中最小值和最大值分别为（ ）
A. y1，y2 B. y43，y44 C. y44，y45 D. y2014，y2015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
