
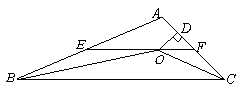
如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .下列四个结论:
.下列四个结论:
![]() ;
;
②以![]() 为圆心、
为圆心、![]() 为半径的圆与以
为半径的圆与以![]() 为圆心、
为圆心、![]() 为半径的圆外切;
为半径的圆外切;
③设![]() 则
则![]() ;
;
④![]() 不能成为
不能成为![]() 的中位线.
的中位线.
其中正确的结论是_____________.(把你认为正确结论的序号都填上)
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
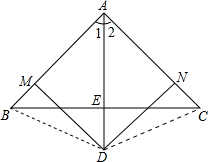 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形
|
查看答案和解析>>
科目:初中数学 来源: 题型:022
(1)在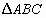 中,
中,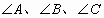 的外角的度数的比是4∶3∶2,那么
的外角的度数的比是4∶3∶2,那么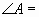 _____度.
_____度.
(2)在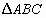 中,
中,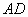 平分
平分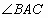 ,如果
,如果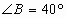 ,
, ,那么
,那么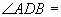 ________度.
________度.
(3)如图,在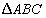 中,
中,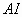 和
和 分别平分
分别平分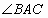 和
和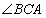 ,如果
,如果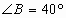 ,那么
,那么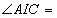 ________度.
________度.
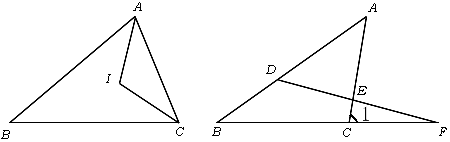
(第(3)题) (第(5)题)
(4)在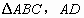 是
是 的平分线,如果
的平分线,如果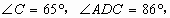 那么
那么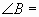 ________度.
________度.
(5)如图,已知 ,那么
,那么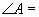 _______度,
_______度, ________度.
________度.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
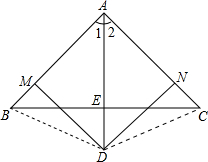 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形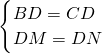 ∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com