
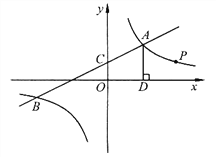
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与y轴交于点C.
,与y轴交于点C.
(1)m= , ![]() = ;
= ;
(2)当x的取值是 时, ![]() >
>![]() ;
;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当![]() :
: ![]() =3:1时,求点P的坐标.
=3:1时,求点P的坐标.
【答案】(1)4, ![]() ;(2)-8<x<0或x>4;(3)P(
;(2)-8<x<0或x>4;(3)P(![]() )
)
【解析】(1)把B点坐标代入![]() ,可求出
,可求出![]() ,再将
,再将![]() 坐标代入可求出m,把A、B两点坐标代入
坐标代入可求出m,把A、B两点坐标代入![]() 即可求出
即可求出![]() 、b;
、b;
(2)由两函数图象的交点坐标,即可得出![]() >
>![]() 的解集;
的解集;
(3)先利用![]() :
: ![]() =3:1求出点E坐标,再用待定系数法求出直线OP的解析式,最后就可求出直线OP与
=3:1求出点E坐标,再用待定系数法求出直线OP的解析式,最后就可求出直线OP与![]() 的图象在第一象限内的交点P
的图象在第一象限内的交点P
解:(1)4, ![]() ;
;
(2)-8<x<0或x>4;
(3)由(1)知, ![]()
∴m=4,点C的坐标是(0,2)点A的坐标是(4,4).
∴CO=2,AD=OD=4.
∴![]()
∵![]() [
[
∴![]()
即![]() OD·DE=4,∴DE=2.
OD·DE=4,∴DE=2.
∴点E的坐标为(4,2).
又点E在直线OP上,∴直线OP的解析式是![]() .
.
∴直线OP与![]() 的图象在第一象限内的交点P的坐标为(
的图象在第一象限内的交点P的坐标为(![]() )
)


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
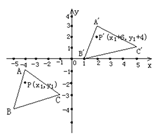
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
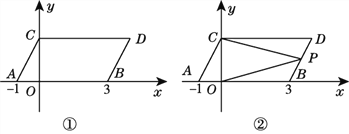
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为多少米?(结果保留整数,测角仪忽略不计, ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com