练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．（1）计算：（$\frac{{a}^{2}b}{-c{d}^{3}}$）3$÷\frac{2a}{{d}^{3}}$•（$\frac{c}{2a}$）2
    （2）解方程：1+$\frac{3}{1-x}$=$\frac{3x}{x-1}$．

    分析 （1）原式先计算乘方运算，再计算乘除运算即可得到结果；
    （2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：（1）原式=-$\frac{{a}^{6}{b}^{3}}{{c}^{3}{d}^{9}}$•$\frac{{d}^{3}}{2a}$•$\frac{{c}^{2}}{4{a}^{2}}$=-$\frac{{a}^{3}{b}^{3}}{8c{d}^{6}}$；
    （2）去分母得：x-1-3=3x，
    解得：x=-2，
    经检验x=-2是分式方程的解．

    点评 此题考查了解分式方程，以及分式的混合运算，解分式方程利用了转化的思想，注意要检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

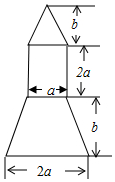    14．2016年10月17日7时30分，神舟十一号飞船顺利升空，同学们倍受鼓舞，开展了火箭模型制作比赛，如图示是火箭模型的截面图，下面是等腰梯形，中间是长方形，上面是一个等腰三角形．
    ①请用含a、b的式子表示该截面面积；
    ②当a=2cm，b=3cm时，求这个火箭模型的截面的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知二次函数的图象的顶点坐标为（-2，$\frac{1}{3}$），且经过点（1，$\frac{10}{3}$），求这个二次函数的表达式及它与y轴的交点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：$\frac{{x}^{-2}-{y}^{-2}}{{x}^{-1}+{y}^{-1}}$+$\frac{1}{y}$-$\frac{1}{x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

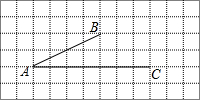    19．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点，已知线段AB、AC的端点都在格点上．
    （1）画图：在AC上标出格点D和E，并连接BD、BE，使得BD⊥AB，BE⊥AC．
    （2）线段BD和BE的大小关系是：BD＞BE（用“＞”或“＜”或“=”填空）．
    （3）图中互余的角共有4对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解下列方程或不等式组
    （1）用配方法解方程：x2-x=3x+5
    （2）解不等式组：$\left\{\begin{array}{l}{x+2＞0}\\{3（x-1）+2≥2x}\end{array}\right.$，并判断-1，$\sqrt{3}$这两个数是否为该不等式组的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

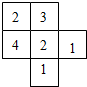    16．如图所示是由若干个大小相同的小立方体所组成几何体从上面看的图，小正方形中的数字表示在该位置的小立方体的个数，请画出这个几何体从正面看到的图，从左面看到的图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

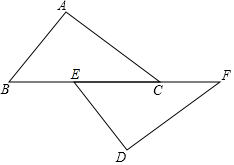    13．如图，已知点B、E、C、F在一条直线上，AC∥DE，AC=DE，∠A=∠D．
    （1）求证：AB=DE；
    （2）若BC=9，EC=5，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知代数式x2-4x+7．
    （1）用配方法将代数式化成（x+p）2+q的形式；
    （2）试说明不论x取何值．这个代数式的值总是正数．

    查看答案和解析>>

    同步练习册答案