
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚRtĄśABCÖĐŁŹĄÏACB=90ŁŹAB=10ŁŹAC=6ŁŹ”ăEĄąF·Ö±đÊDZßACĄąBCÉϔĶŻ”㣏čę”ăEŚśEDĄÍABÓÚ”ăDŁŹčę”ăFŚśFGĄÍABÓÚ”ăGŁŹDG”Äł€ÊŒÖŐÎȘ2Łź
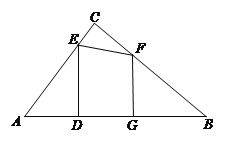
Łš1Ł©”±AD=3ʱŁŹÇóDE”Äł€Ł»
Łš2Ł©”±”ăEĄąFÔÚ±ßACĄąBCÉÏÒƶŻÊ±ŁŹÉè![]() ŁŹÇóyčŰÓÚx”ÄșŻÊęœâÎöÊœŁŹČąĐŽłöșŻÊę”ĶšÒćÓòŁ»
ŁŹÇóyčŰÓÚx”ÄșŻÊęœâÎöÊœŁŹČąĐŽłöșŻÊę”ĶšÒćÓòŁ»
Łš3Ł© ÔÚ”ăEĄąFÒƶŻčęłÌÖĐŁŹĄśAEDÓ륜CEFÄÜ·ńÏàËÆŁŹÈôÄÜŁŹÇóAD”Äł€Ł»ÈôČ»ÄÜŁŹÇë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄżŁš1Ł©DE=4Ł»Łš2Ł©![]() Ł»Łš3Ł©”±AD”Äł€ÎȘ
Ł»Łš3Ł©”±AD”Äł€ÎȘ![]() »ò
»ò![]() ʱŁŹĄśAEDÓ륜CEFÏàËÆ.
ʱŁŹĄśAEDÓ륜CEFÏàËÆ.
ĄŸœâÎöĄż
Łš1Ł©žùŸĘčŽčɶšÀíÏÈÇółöBC”Äł€ŁŹÔÙÍščęրÜĄśADEĄŚĄśACBŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊ”ĂłöDE”Äł€Ł»
Łš2Ł©ÍščęրÜĄśBGFĄŚĄśBCAŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊ”ĂłöyčŰÓÚx”ÄșŻÊęœâÎöÊœŁ»
Łš3Ł©ÓÉŁš1Ł©Łš2Ł©żÉ”ĂŁș![]() ŁŹ·ÖĄÏA=ĄÏCEFŁŹĄÏA=ĄÏCFEÁœÖÖÇéżöÇółöĄśAEDÓ륜CEFÏàËÆʱAD”Äł€Łź
ŁŹ·ÖĄÏA=ĄÏCEFŁŹĄÏA=ĄÏCFEÁœÖÖÇéżöÇółöĄśAEDÓ륜CEFÏàËÆʱAD”Äł€Łź
œâŁșŁš1Ł©ĄßĄÏACB=90ĄăŁŹAB=10ŁŹAC=6
ĄàBC=8Łš1·ÖŁ©
ĄßEDĄÍABĄàĄÏADE=ĄÏACB=90Ąă
Ó֥ߥÏA=ĄÏA
ĄàĄśADEĄŚĄśACB
![]()
ĄàDE=4Ł»
Łš2Ł©ĄßFGĄÍABĄàĄÏBGF=ĄÏBCA=90Ąă
Ó֥ߥÏB=ĄÏB
ĄàĄśBGFĄŚĄśBCA
![]()
![]()
![]() Ł»
Ł»
Łš3Ł©ÓÉŁš1Ł©Łš2Ł©żÉ”ĂŁș![]()
![]()
”±ĄÏA=ĄÏCEFʱŁŹ![]() œâ”ĂŁș
œâ”ĂŁș![]()
”±ĄÏA=ĄÏCFEʱŁŹ![]() œâ”ĂŁș
œâ”ĂŁș![]()
Ąà”±AD”Äł€ÎȘ![]() »ò
»ò![]() ʱŁŹĄśAEDÓ륜CEFÏàËÆŁź
ʱŁŹĄśAEDÓ륜CEFÏàËÆŁź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄł°àĄ°ÊęѧĐËÈ€ĐĄŚéĄ±¶ÔșŻÊęy=x2©2|x|”ÄÍŒÏóșÍĐÔÖÊœűĐĐÁËÌœŸżŁŹÌœŸżčęłÌÈçÏÂŁŹÇëČčłäÍêŐûŁźŁš1Ł©ŚÔ±äÁżx”ÄÈĄÖ”·¶Î§ÊÇÈ«ÌćÊ”Ê꣏xÓëy”ÄŒžŚé¶ÔÓŠÖ”ÁбíÈçÏÂŁș
x | Ą | ©3 | © | ©2 | ©1 | 0 | 1 | 2 |
| 3 | Ą |
y | Ą | 3 |
| m | ©1 | 0 | ©1 | 0 |
| 3 | Ą |
ÆäÖĐŁŹm=ĄĄĄĄŁź
Łš2Ł©žùŸĘ±íÖĐÊęŸĘŁŹÔÚÈçÍŒËùÊŸ”ÄÆœĂæÖ±œÇŚű±êÏ”ÖĐĂè”㣏ȹ»łöÁËșŻÊęÍŒÏó”ÄÒ»Čż·ÖŁŹÇ뻳öžĂșŻÊęÍŒÏó”ÄÁíÒ»Čż·ÖŁź
Łš3Ł©čÛČìșŻÊęÍŒÏóŁŹĐŽłöÁœÌőșŻÊę”ÄĐÔÖÊŁź
Łš4Ł©œűÒ»ČœÌœŸżșŻÊęÍŒÏó·ąÏÖŁș
ąÙșŻÊęÍŒÏóÓëxÖáÓĐĄĄĄĄžöœ»”㣏ËùÒÔ¶ÔÓŠ”Ä·œłÌx2©2|x|=0ÓĐĄĄ ĄĄžöÊ”ÊęžùŁ»
ąÚ·œłÌx2©2|x|=2ÓĐĄĄĄĄžöÊ”Êęžù.

ąÛčŰÓÚx”Ä·œłÌx2©2|x|=aÓĐ4žöÊ”ÊęžùʱŁŹa”ÄÈĄÖ”·¶Î§ÊÇĄĄ Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎÊÌâŁșŁš1Ł©ÈçÍŒąÙŁŹÔÚRtĄśABCÖĐŁŹABŁœACŁŹDÎȘBC±ßÉÏÒ»”㣚ȻÓë”ăBŁŹCÖŰșÏŁ©ŁŹœ«Ï߶ÎADÈÆ”ăAÄæʱŐëĐęŚȘ90Ąă”Ă”œAEŁŹÁŹœÓECŁŹÔòÏ߶ÎBCŁŹDCŁŹECÖźŒäÂúŚă”Ä”ÈÁżčŰϔʜÎȘĄĄ ĄĄŁ»
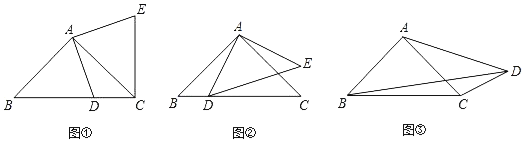
ÌœËśŁșŁš2Ł©ÈçÍŒąÚŁŹÔÚRtĄśABCÓëRtĄśADEÖĐŁŹABŁœACŁŹADŁœAEŁŹœ«ĄśADEÈÆ”ăAĐęŚȘŁŹÊč”ăDÂäÔÚBC±ßÉÏŁŹÊÔÌœËśÏ߶ÎADŁŹBDŁŹCDÖźŒäÂúŚă”Ä”ÈÁżčŰÏ”ŁŹČąÖ€ĂśÄă”ÄœáÂÛŁ»
ÓŠÓĂŁșŁš3Ł©ÈçÍŒąÛŁŹÔÚËıßĐÎABCDÖĐŁŹĄÏABCŁœĄÏACBŁœĄÏADCŁœ45ĄăŁźÈôBDŁœ9ŁŹCDŁœ3ŁŹÇóAD”Äł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»ŽÎșŻÊę![]() Óë·Ž±ÈÀęșŻÊę
Óë·Ž±ÈÀęșŻÊę![]() ”ÄÍŒÏóœ»ÓÚ
”ÄÍŒÏóœ»ÓÚ![]() Áœ”㣏čę”ă
Áœ”㣏čę”ă![]() Śś
Śś![]() ÖᣏŽčŚăÎȘ”ă
ÖᣏŽčŚăÎȘ”ă![]() ŁŹÇÒ
ŁŹÇÒ![]() ĄŁ
ĄŁ
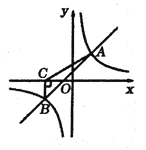
Łš1Ł©ÇóÒ»ŽÎșŻÊęÓë·Ž±ÈÀęșŻÊę”ıíŽïÊœŁ»
Łš2Ł©žùŸĘËùžűÌőŒțŁŹÇëÖ±œÓĐŽłöČ»”ÈÊœ![]() ”ÄœâŒŻŁ»
”ÄœâŒŻŁ»
Łš3Ł©Èô![]() ÊÇ·Ž±ÈÀęșŻÊę
ÊÇ·Ž±ÈÀęșŻÊę![]() ÍŒÏóÉÏ”ÄÁœ”㣏ÇÒ
ÍŒÏóÉÏ”ÄÁœ”㣏ÇÒ![]() ŁŹÇóÊ”Êę
ŁŹÇóÊ”Êę![]() ”ÄÈĄÖ”·¶Î§ĄŁ
”ÄÈĄÖ”·¶Î§ĄŁ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
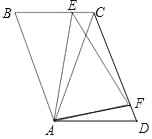
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĐĐËıßĐÎABCDÖĐŁŹAC=CDŁŹÈô”ăEĄąF·Ö±đÎȘ±ßBCĄąCDÉÏ”ÄÁœ”㣏ÇÒĄÏEAF=ĄÏCADŁź
Łš1Ł©ÇóÖ€ŁșĄśADFĄŚĄśACEŁ»
Łš2Ł©ÇóÖ€ŁșAE=EFŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÖ±Ïßy=-x+2·Ö±đœ»xÖ᥹yÖáÓÚ”ăAŁŹBŁŹ”ăDÔÚBA”ÄŃÓł€ÏßÉÏŁŹOD”ÄŽčֱƜ·ÖÏßœ»Ï߶ÎABÓÚ”ăCŁźÈôĄśOBCșÍĄśOAD”ÄÖÜł€Ïà”ÈŁŹÔòOD”Äł€ÊÇ( )
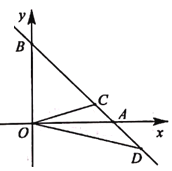
A. 2B. 2![]() C.
C. ![]() D. 4
D. 4
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏßy=-x2+4x-1ÓëyÖ᜻ÓÚ”ăCŁŹCDĄÎxÖáœ»ĆŚÎïÏßÓÚÁíÒ»”ăDŁŹABĄÎxÖáœ»ĆŚÎïÏßÓÚ”ăAŁŹBŁŹ”ăAÔÚ”ăB”ÄŚóČàŁŹÇÒÁœ”ăŸùÔÚ”ÚÒ»ÏóÏȚŁŹBHĄÍCDÓÚ”ăHŁźÉè”ăA”ÄșáŚű±êÎȘmŁź
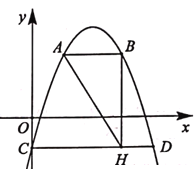
Łš1Ł©”±m=1ʱŁŹÇóAB”Äł€.
Łš2Ł©ÈôAH=![]() ŁšCH-DHŁ©ŁŹÇóm”ÄÖ”.
ŁšCH-DHŁ©ŁŹÇóm”ÄÖ”.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĐĐËıßĐÎ![]() ÖĐŁŹ
ÖĐŁŹ![]() Ąą
Ąą![]() Ïàœ»ÓÚ”ă
Ïàœ»ÓÚ”ă![]() ŁŹ”ă
ŁŹ”ă![]() ÊÇ
ÊÇ![]() ”ÄÖД㣏ÁŹœÓ
”ÄÖД㣏ÁŹœÓ![]() ČąŃÓł€œ»
ČąŃÓł€œ»![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹ
ŁŹ![]() ŁŹÔòÏÂÁĐœáÂÛŁșąÙ
ŁŹÔòÏÂÁĐœáÂÛŁșąÙ![]() Ł»ąÚ
Ł»ąÚ![]() Ł»ąÛ
Ł»ąÛ![]() Ł»ąÜ
Ł»ąÜ![]() ŁŹÆäÖĐÒ»¶šŐęÈ·”ÄÊÇ(ĄĄĄĄ)Łź
ŁŹÆäÖĐÒ»¶šŐęÈ·”ÄÊÇ(ĄĄĄĄ)Łź
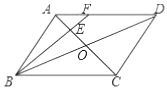
A.ąÙąÚąÛąÜB.ąÙąÚC.ąÚąÛąÜD.ąÙąÚąÛ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÖ±Ïß![]() ÓëxÖ᥹yÖá·Ö±đœ»ÓÚAĄąBÁœ”㣏”ăPŽÓ”ăAłö·ąŁŹŃŰŐÛÏßAB©BOÏòÖŐ”ăOÔ˶ŻŁŹÔÚABÉÏÒÔĂżĂë5žö”„λł€¶È”ÄËÙ¶ÈÔ˶ŻŁŹÔÚBOÉÏÒÔĂżĂë3žö”„λł€¶È”ÄËÙ¶ÈÔ˶Ż;”ăQŽÓ”ăOłö·ąŁŹŃŰOA·œÏòÒÔĂżĂë
ÓëxÖ᥹yÖá·Ö±đœ»ÓÚAĄąBÁœ”㣏”ăPŽÓ”ăAłö·ąŁŹŃŰŐÛÏßAB©BOÏòÖŐ”ăOÔ˶ŻŁŹÔÚABÉÏÒÔĂżĂë5žö”„λł€¶È”ÄËÙ¶ÈÔ˶ŻŁŹÔÚBOÉÏÒÔĂżĂë3žö”„λł€¶È”ÄËÙ¶ÈÔ˶Ż;”ăQŽÓ”ăOłö·ąŁŹŃŰOA·œÏòÒÔĂżĂë![]() žö”„λł€¶È”ÄËÙ¶ÈÔ˶Ż.PŁŹQÁœ”ăÍŹÊ±łö·ąŁŹ”±”ăPÍŁÖčʱŁŹ”ăQÒČËæ֟ͣÖč.čę”ăPŚśPEĄÍAOÓÚ”ăEŁŹÒÔPEŁŹEQÎȘÁڱߌśŸŰĐÎPEQFŁŹÉèŸŰĐÎPEQFÓ륜ABOÖŰ”țČż·ÖÍŒĐΔÄĂæ»ęÎȘS,”ăPÔ˶Ż”ÄʱŒäÎȘtĂë.
žö”„λł€¶È”ÄËÙ¶ÈÔ˶Ż.PŁŹQÁœ”ăÍŹÊ±łö·ąŁŹ”±”ăPÍŁÖčʱŁŹ”ăQÒČËæ֟ͣÖč.čę”ăPŚśPEĄÍAOÓÚ”ăEŁŹÒÔPEŁŹEQÎȘÁڱߌśŸŰĐÎPEQFŁŹÉèŸŰĐÎPEQFÓ륜ABOÖŰ”țČż·ÖÍŒĐΔÄĂæ»ęÎȘS,”ăPÔ˶Ż”ÄʱŒäÎȘtĂë.
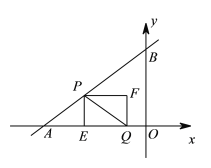
(1)ÁŹœáPQŁŹ”±PQÓ륜ABO”ÄÒ»±ßÆœĐĐʱŁŹÇót”ÄÖ”;
(2)ÇóSÓëtÖźŒä”ÄșŻÊęčŰϔʜ,ČąÖ±œÓĐŽłöŚÔ±äÁżt”ÄÈĄÖ”·¶Î§.
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com