分析:先根据负整数指数幂和乘方的意义可计算出
|-|+()2-(3.14-π)3-2-1≈
+
-0-
=
;然后分别根据一次函数图象计算四个图象中的阴影图形的面积:如图1,S
阴影可近似看作S
正方形PHOG,S
阴影=1;如图2,先确定P点坐标为(1,3),可计算出S
阴影=
;如图3直接计算出S
阴影=1;如图4,先确定P点、E点和F点坐标,然后根据三角形面积公式得到S
阴影=1;最后根据计算结果进行判断.
解答:解:
|-|+()2-(3.14-π)3-2-1≈
+
-0-
=
.
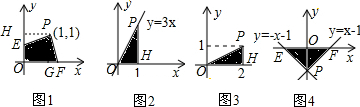
如图1,过P点作PH⊥y轴,PG⊥x轴,则S
阴影可近似看作S
正方形PHOG,
∵P点坐标为(1,1),
∴S
阴影=1×1=1;
如图2,当x=1时,y=3x=3,
∴P点坐标为(1,3),
∴S
阴影=
×1×3=
;
如图3,S
阴影=
×1×2=1;
如图4,把x=0代入y=x-1和y=-x-1都得y=-1,则P点坐标为(0,-1),
把y=0代入y=-x-1得-x-1=0,解得x=-1;把y=0代入y=x-1得x-1=0,解得x=1,
∴E点坐标为(-1,0),F点坐标为(1,0),
∴S
阴影=
×1×2=1.
故选B.
点评:本题考查了一次函数的综合题:一次函数图象上点的坐标满足其解析式;会结合图形分析其中的几何图形,再利用点的坐标求出面积.也考查了负整数指数幂.

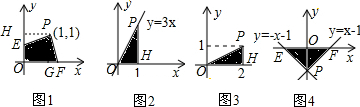 如图1,过P点作PH⊥y轴,PG⊥x轴,则S阴影可近似看作S正方形PHOG,
如图1,过P点作PH⊥y轴,PG⊥x轴,则S阴影可近似看作S正方形PHOG,