
如图19,E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点,每组对边上的两个点,可以连接成一条线段.
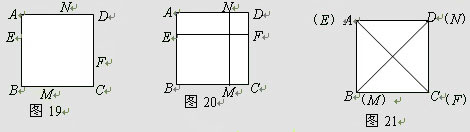
(1)如图20,如果EF∥BC,MN∥CD,那么EF MN(位置),EF MN(大小)
(2)如图21,如果E与A,F与C,M与B,N与D重合,那么EF MN(位置),EF MN(大小).
(3)当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想.
科目:初中数学 来源: 题型:
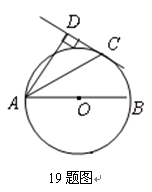
如图19,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
1.求证:AC平分∠DAB
2.过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
3.若CD=4,AC=4,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届山东省宁津县实验中学九年级中考模拟数学试卷(带解析) 题型:解答题
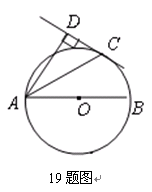
如图19,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
【小题1】求证:AC平分∠DAB
【小题2】过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
【小题3】若CD=4,AC=4,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考模拟数学试卷(解析版) 题型:解答题
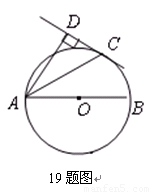
如图19,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
1.求证:AC平分∠DAB
2.过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
3.若CD=4,AC=4,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源:2011年辽宁省凌海市初二年上学期期末数学卷 题型:解答题
如图19,E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点,每组对边上的两个点,可以连接成一条线段.
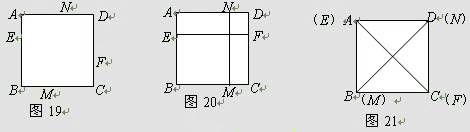
(1)如图20,如果EF∥BC,MN∥CD,那么EF MN(位置),EF MN(大小)
(2)如图21,如果E与A,F与C,M与B,N与D重合,那么EF MN(位置),EF MN(大小).
(3)当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com