
【题目】科技改变世界.随着科技的发展,自动化程度越来越高,机器人市场越来越火.某商场购进一批![]() ,
,![]() 两种品牌的编程机器人,进价分别为每台3000元、4000元.市场调查发现:销售3个
两种品牌的编程机器人,进价分别为每台3000元、4000元.市场调查发现:销售3个![]() 品牌机器人和2个
品牌机器人和2个![]() 品牌机器人,可获利润6000元;销售2个
品牌机器人,可获利润6000元;销售2个![]() 品牌机器人和3个
品牌机器人和3个![]() 品牌机器人,可获利润6500元.
品牌机器人,可获利润6500元.
(1)此商场![]() .
.![]() 两种品牌的编程机器人销售价格分别是多少元?
两种品牌的编程机器人销售价格分别是多少元?
(2)若商场准备用不多于65000元的资金购进![]() ,
,![]() 两种品牌的编程机器人共20个,则至少需要购进
两种品牌的编程机器人共20个,则至少需要购进![]() 品牌的编程机器人多少个?
品牌的编程机器人多少个?
(3)不考虑其它因素,商场打算![]() 品牌编程机器人数量不多于
品牌编程机器人数量不多于![]() 品牌编程机器人数量的
品牌编程机器人数量的![]() ,现打算购进
,现打算购进![]() ,
,![]() 两种品牌编程机器人共40个,怎样进货才能获得最大的利润?
两种品牌编程机器人共40个,怎样进货才能获得最大的利润?
【答案】(1)商场![]() 、
、![]() 两种品牌的编程机器人销售价格分别是4000元、5500元;(2)至少为15个;(3)购进
两种品牌的编程机器人销售价格分别是4000元、5500元;(2)至少为15个;(3)购进![]() 品牌编程机器人27个,
品牌编程机器人27个,![]() 品牌编程机器人13个能获得最大的利润.
品牌编程机器人13个能获得最大的利润.
【解析】
(1)设商场![]() 、
、![]() 两种品牌的编程机器人销售价格分别是
两种品牌的编程机器人销售价格分别是![]() 元、
元、![]() 元,根据题意列出方程组,解之即可;
元,根据题意列出方程组,解之即可;
(2)设需要购进![]() 品牌的编程机器人
品牌的编程机器人![]() 个,根据商场准备用不多于65000元的资金购进
个,根据商场准备用不多于65000元的资金购进![]() ,
,![]() 两种品牌的编程机器人共20个列出不等式,求解;
两种品牌的编程机器人共20个列出不等式,求解;
(3)设需要购进![]() 品牌的编程机器人
品牌的编程机器人![]() 个.利润为
个.利润为![]() 元,得出
元,得出![]() 和b的关系式,再根据
和b的关系式,再根据![]() 品牌编程机器人数量不多于
品牌编程机器人数量不多于![]() 品牌编程机器人数量的
品牌编程机器人数量的![]() 求出b的取值范围,从而求出当b=13时,获得最大利润.
求出b的取值范围,从而求出当b=13时,获得最大利润.
解:(1)设商场![]() 、
、![]() 两种品牌的编程机器人销售价格分别是
两种品牌的编程机器人销售价格分别是![]() 元、
元、![]() 元.
元.
根据题意列方程组得:
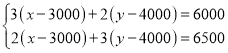 ,
,
解得:![]() ,
,
答:此商场A,B两种品牌的编程机器人销售价格分别是4000元,5500元.
(2)设需要购进![]() 品牌的编程机器人
品牌的编程机器人![]() 个.
个.
根据题意得: ![]()
解得:![]()
∵![]() 为编程机器人的个数
为编程机器人的个数
∴![]() 为
为![]() 的整数
的整数
∴至少为15个
答:至少需要购进![]() 品牌的编程机器人15个.
品牌的编程机器人15个.
(3)设需要购进![]() 品牌的编程机器人
品牌的编程机器人![]() 个.利润为
个.利润为![]() 元.
元.
根据题意得:![]()
![]()
根据题意得: ![]()
解得:![]()
∵![]()
∴![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 最大时
最大时![]() 最大
最大
∴![]() 的最大整数
的最大整数
∴![]()
则![]()
答:购进![]() 品牌编程机器人27个,
品牌编程机器人27个,![]() 品牌编程机器人13个能获得最大的利润.
品牌编程机器人13个能获得最大的利润.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
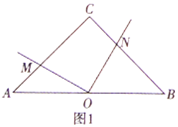
【题目】问题发现:(1)如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交
交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的数量关系为____;
的数量关系为____;
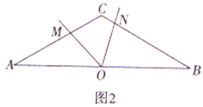
问题探究:(2)如图2,在等腰三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交
交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的数量关系是否改变,请说明理由;
的数量关系是否改变,请说明理由;
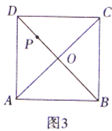
问题解决:(3)如图3,点![]() 为正方形
为正方形![]() 对角线的交点,点
对角线的交点,点![]() 为
为![]() 的中点,点
的中点,点![]() 为直线
为直线![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,当
,当![]() 面积为
面积为![]() 时,直接写出线段
时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,聪聪想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离(AB)为16m,又测得从A处看建筑物底部C的俯角α为30°,看建筑物顶部D的仰角β为53°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
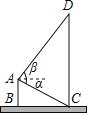
(1)求AB与CD之间的距离(结果保留根号).
(2)求建筑物CD的高度(结果精确到1m).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
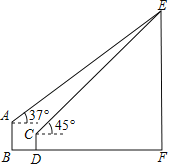
【题目】如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 位于其北偏东
位于其北偏东![]() 方向上,轮船沿正东方向航行20海里到达
方向上,轮船沿正东方向航行20海里到达![]() 处后,测得灯塔
处后,测得灯塔![]() 位于其北偏东
位于其北偏东![]() 方向上,轮船沿计划路线航行时与灯塔
方向上,轮船沿计划路线航行时与灯塔![]() 的距离最少是_______海里.(结果保留根号)
的距离最少是_______海里.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
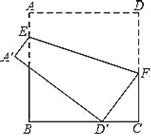
【题目】如图,正方形![]() 的边长是9,点
的边长是9,点![]() 是
是![]() 边上的一个动点,点
边上的一个动点,点![]() 是
是![]() 边上一点,
边上一点,![]() ,连接
,连接![]() ,把正方形
,把正方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
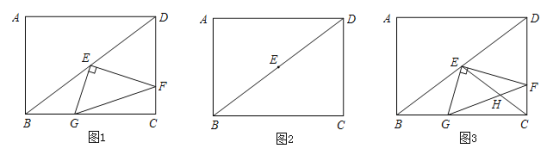
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是对角线BD的中点,直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G.
(1)若点F是边CD的中点,求EG的长.
(2)当直角∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC交于点F、G.∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值.
(3)当直角∠GEF绕顶点E旋转,旋转过程中与边CD、BC所在的直线交于点F、G.在图2中画出图形,并判断∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请直接写出tan∠EFG的值.
(4)如图3,连接CE交FG于点H,若![]() ,请求出CF的长.
,请求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
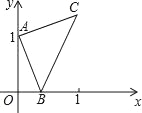
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. 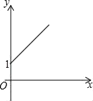 B.
B. 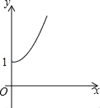 C.
C. 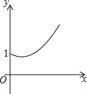 D.
D. 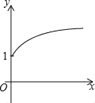
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com